1.4 支持向量机¶

支持向量机(SVMs)是一种用于分类、回归和异常检测的有监督学习方法。

支持向量机的优点有：

在高维空间里也非常有效
对于数据维度远高于数据样本量的情况也有效
在决策函数中使用训练集的子集(也称为支持向量)，因此也是内存高效利用的。
通用性：可以为决策函数指定不同的核函数。已经提供了通用核函数，但也可以指定自定义核函数。

支持向量机的缺点包括：

如果特征数量远远大于样本数，则在选择核函数和正则化项时要避免过度拟合。
SVMs不直接提供概率估计，这些计算使用昂贵的五倍交叉验证(见分数和概率)。

scikit-learn中的支持向量机-同时支持稠密(dense)(numpy.ndarray和可通过numpy.asarray转换)和稀疏(sparse)(任意的scipy.sparse)样本向量作为输入。然而，若要使用支持向量机对稀疏数据进行预测，则必须在这样的数据上进行拟合。要获得最佳性能，可使用C_ordered的numpy.ndarray对象(稠密 dense)，或者使用数据类型是dtype=float64的 scipy.sparse.csr_matrix 对象(稀疏 sparse)。

1.4.1 分类

SVC、NuSVC和LinearSVC能够在数据集上执行多分类。

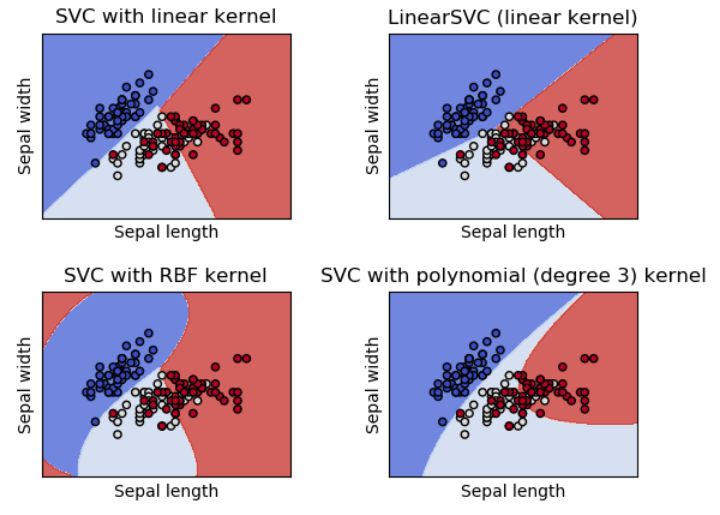SVC 和 NuSVC是相似的方法，但是接受的参数的集合稍微不同并且有不同的数学公式(看这部分数学公式)。另一方面， LinearSVC是使用线性核的支持向量分类的的另一种实现, 适用于线性核的情况。注意，LinearSVC不接受关键字内核，因为假设是线性的。它还缺少 SVC 和 NuSVC 的一些属性，如Support_。

和其他分类器一样， SVC, NuSVC 和 LinearSVC需要两个数组作为输入， [n_samples, n_features]尺寸的数组X作为训练样本，, [n_samples] 大小的数组 y 作为类别标签(字符串或者整数):

>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC()
>>> clf.fit(X, y)
SVC()

经拟合后，该模型可用于预测新的值：

>>> clf.predict([[2., 2.]])
array([1])

SVMs的决策函数依赖于训练数据的某些子集，被称为支持向量。这些支持向量的一些特性可以在属性 support_vectors_, support_ 和 n_support中找到：

>>> # 获取支持向量
>>> clf.support_vectors_
array([[0., 0.],
       [1., 1.]])
>>> # 获取支持向量的索引
>>> clf.support_
array([0, 1]...)
>>> # 获取每个类中支持向量的个数
>>> clf.n_support_
array([1, 1]...)

Examples:

支持向量机：最大边距分离超平面,
非线性支持向量机
支持向量机方差分析：一元特征选择的支持向量机,

1.4.1.1 多分类

SVC和NuSVC 为实现多分类的使用了“一对一”的方法(Knerr等人，1990年)。如果n_class是类别的数量，那么 n_class * (n_class - 1) / 2 分类器会被重构，每个分类器都是使用两类数据进行训练。为了提供与其他分类器一致的接口， decision_function_shape选项允许将“一对一”分类器的结果转换为形状是(n_samples, n_classes)的决策函数。

>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(decision_function_shape='ovo')
>>> clf.fit(X, Y)
SVC(decision_function_shape='ovo')
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4

另一方面，LinearSVC实现了“one-vs-the-rest”的多类策略，从而训练了n_class（n 类别）个模型。如果只有两个类，则只训练一个模型：

>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y)
LinearSVC()
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4

有关决策函数的完整描述，请参见数学公式 Mathematical formulation。

请注意，LinearSVC还实现了另一种多分类策略，即由Crammer和Singerr [16]提出的所谓的多分类支持向量机，它使用的选项是multiclass=‘sammer_singer’。此方法是一致的，对于one-vs-rest 分类准确度一般是不够的。在实践中，one-vs-rest分类通常是首选的，因为结果大多是差不多的，但运行时间要少得多。

对于“one-vs-rest”的LinearSVC，它的属性coef_ and intercept_ 分别拥有的形状是 [n_class, n_features] 和[n_class]。系数的每一行对应于n_class这么多个“one-vs-rest”分类器中的一个，在按照 'one'类的排序下，和intercepts相似。

在“one-vs-one” 的 SVC情况下，属性的布局更复杂一些。在具有线性核的情况下，属性 coef_ 和intercept_ 分别具有[n_class * (n_class - 1) / 2, n_features]和 [n_class * (n_class - 1) / 2]的形状。这与上面描述的LinearSVC的布局类似，每一行现在对应于二分类器。0到n的类排序是 “0 vs 1”, “0 vs 2” , … “0 vs n”, “1 vs 2”, “1 vs 3”, “1 vs n”, . . . “n-1 vs n”。

dual_coef_的形状是 [n_class-1, n_SV], 有点难以理解这个布局。它的列是对应 n_class * (n_class - 1) / 2这么多个 “one-vs-one”分类器中的任意一个。每个支持向量都使用在n_class-1个分类器中。

可以通过一个例子更清楚地说明这一点：

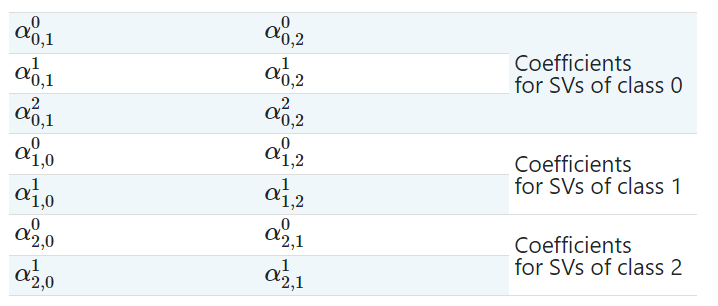
考虑一个三分类的问题， 0类有三个支持向量, 并且1类和2类分别有两个支持向量和。对于每一个支持向量来说，都有两个对偶系数。我们称类和中支持向量的系数为，对偶系数dual_coef_如下：

示例
在iris数据集中绘制不同的SVM分类器

1.4.1.2 分数和概率

SVC 和 NuSVC 的decision_function决策函数给出了每个样本的每类分数(或者是一个二分类情况下给每一个样本一个简单的分数)，当把参数probability设置为True的时候，就会启用类成员概率估计(可从方法predict_proba和predict_log_proba获得)。在二分类情况下，概率用Platt scaling进行标准化 [9]：对支持向量机的分数进行Logistic回归，通过对训练数据的额外交叉验证来拟合。在多类的情况下，这会扩展为per [10]。

注意：所有的估计器都可以通过 CalibratedClassifierCV (看 Probability calibration)来使用相同的概率校准过程。在SVC和NuSVC的情况下，在底层中是使用libsvm中构建的，因此它不依赖Scikit-Learning的类CalibratedClassifierCV。

Platt校准所涉及的交叉验证对于大型数据集来说是一项昂贵的操作。此外，概率估计可能与分数不一致：

分数的 “argmax” 可能不是概率的 “argmax”
在二分类中，即使predict_proba的输出小于0.5，样本也可以被预测为属于正类；同样，即使predict_proba的输出大于0.5，它也可以被标记为负类。

Platt这个方法也有理论上的问题。如果需要置信度分数，但这些不一定是概率，那么最好设置probability=False，使用decision_function来代替 predict_proba。

请注意，当DecisionFunctionShape=‘ovr’和n_class>2时，与decision_function不同的是，预测方法在默认情况下不会试图中断联系。您可以为predict的输出设置break_ties=True，使其与np.argmax(clf.Decisionfunction(...)，axis=1)相同，否则始终会返回绑定类中的第一个类;但是要记住，它是有计算成本的。参看支持向量机的练习。

1.4.1.3 非均衡问题

在需要对某些类或个别样本给予更多权重的问题中，可以使用参数class_weight或者sample_weight。

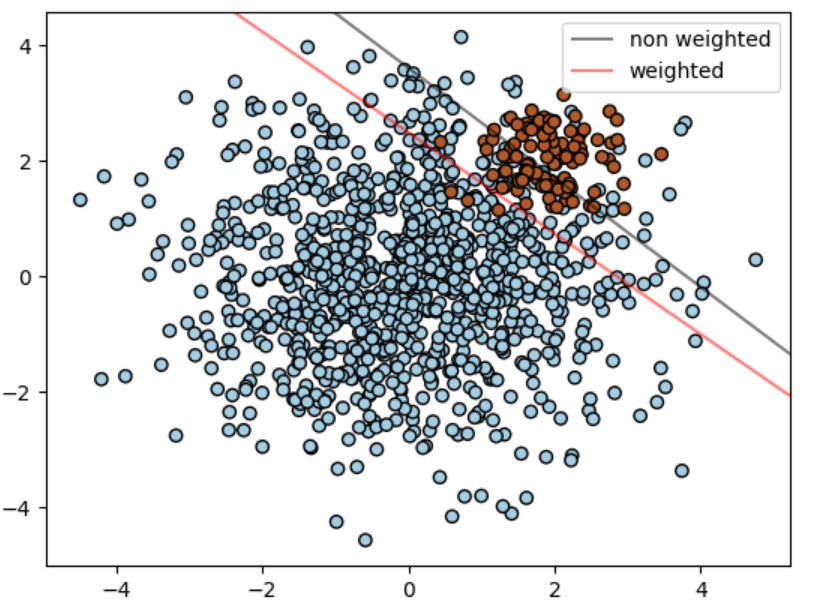
SVC (而不是NuSVC) 是在fit方法中生成了一个关键字class_weight。它是形如{class_Label：value}的字典，其中value是一个大于0的浮点数，它将指定类class_label的参数C设置为C*value。下图是一个不平衡问题的有没有权重校正的插图。

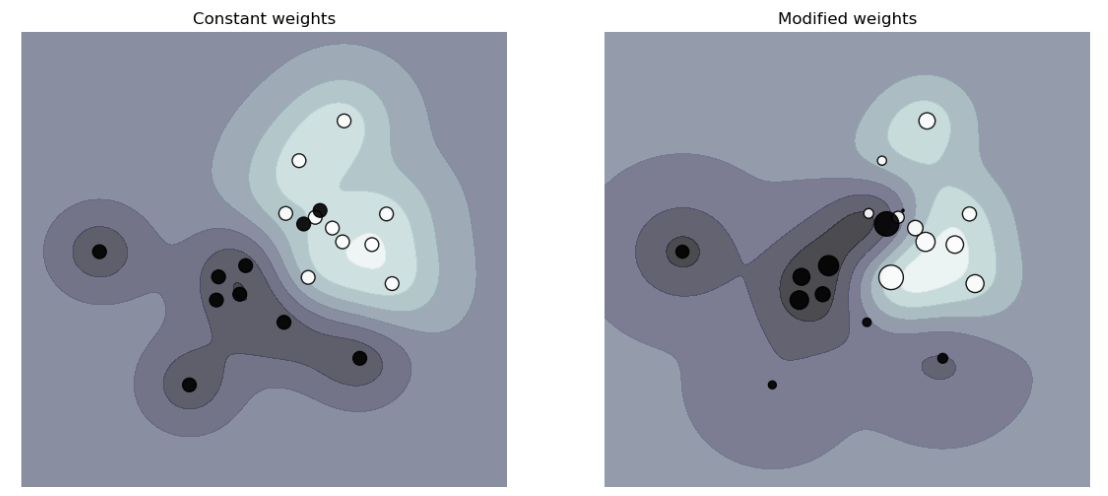
SVC, NuSVC, SVR, NuSVR, LinearSVC, LinearSVR 和 OneClassSVM 是在fit方法中通过参数 sample_weight对单个样本的权重。类似于class_weight，这将把第i个样例的参数c设置为c * sample_weight[i], 这将鼓励分类器正确的获取这些样本。下图说明了样本加权对决策边界的影响。圆圈的大小与样本权重成正比：

示例
支持向量机：不平衡类的分离超平面加权样本

1.4.2 回归

支持向量分类方法可以推广到解决回归问题。这种方法称为支持向量回归。

支持向量分类(如上所述)生成的模型仅依赖于训练数据的一个子集，因为构建模型的成本函数(cost funtion)并不关心超出边际(margin)的训练点。类似地，支持向量回归模型仅依赖于训练数据的一个子集，因为成本函数忽略了预测接近目标对象的样本。

支持向量回归有三种不同的实现方式：SVR、NuSVR和LinearSVR。LinearSVR提供了比SVR更快的实现，但只考虑了线性内核，而NuSVR实现的方式与SVR和LinearSVR略有不同。有关更多详细信息，详细信息请参见Implementation details。

与分类的类一样，fit方法将把向量X，y作为参数向量，只是在这种情况下，只在 y 是浮点数而不是整数型:

>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> regr = svm.SVR()
>>> regr.fit(X, y)
SVR()
>>> regr.predict([[1, 1]])
array([1.5])

示例
基于线性和非线性核的支持向量回归(SVR)

1.4.3 密度估计，异常检测

类OneClassSVM实现了一种用于离群点检测的单类支持向量机.

关于OneClassSVM的描述与使用，请看 Novelty and Outlier Detection。

1.4.4 复杂度

支持向量机是一种强大的工具，但是它们的计算和存储需求随着训练向量的增加而迅速增加。支持向量机的核心是二次规划问题(QP)，它将支持向量从其余的训练数据中分离出来。在实践中(数据集相关)，会根据 libsvm 的缓存的效率，在和之间基于 libsvm 的缩放操作才会调用这个 QP 解析器。如果数据是非常稀疏的，则应该用样本向量中非零特征的平均数量来替换。

对于线性情况，通过 liblinear实现的 LinearSVC算法比基于 libsvm的SVC算法要高效得多，并且可以线性地扩展到数百万个样本和/或特征。

1.4.5 实用技巧

避免数据复制：对于SVC、SVR、NuSVC和NuSVR，如果传递给某些方法的数据不是行优先级(C-ordered)的和双重精度的，则在调用底层C实现之前将复制它。您可以通过检查给定的numpy数组的flags属性来检查它是否是行优先级的。

对于 LinearSVC(和 LogisticRegression)，作为numpy数组传递的任何输入都将被复制并转换为 liblinear 库内部稀疏数据表示(双精度浮点数和非零部分的int 32索引)。如果您想在拟合一个大型的线性分类器，但是又不打算以一个稠密的行优先级的双精度数组作为输入，那我们建议您使用SGDClassifier类来代替。目标函数可以配置为几乎与 LinearSVC模型相同。
内核缓存大小：对于SVC、SVR、NuSVC和NuSVR，内核缓存的大小对大规模问题的运行时间有很大的影响。如果您有足够的可用RAM，建议将cache_size设置为比默认值200(MB)更高的值，例如500(MB)或1000(MB)。
设置C: C默认为1，这是一个合理的默认选择。如果观测数据有大量的噪声，你应该调小它：调小C对应于增强的正则化。

当C值较较大时，LinearSVC 和 LinearSVR对C不太敏感，预测结果在C值大于一定阈值后停止提高。同时，较大的C值将需要更多的时间来训练，有时要花费10倍的时间，就如同这里描述的一样[11]。
支持向量机算法不能是很好的容忍非标准化数据，所以我们强烈建议标准化你的数据。例如，将输入向量X上的每个属性缩放为[0，1]或[-1，+1]，或将其标准化为均值为0和方差为1。注意，同样的缩放必须应用于测试集向量以获得有意义的结果。使用 Pipeline可以很容易地完成任务：

>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.svm import SVC

>>> clf = make_pipeline(StandardScaler(), SVC())

有关缩放和标准化的更多详细信息，请参阅 Preprocessing data一节。

对于参数shrinking, 引用[12]：我们发现如果迭代次数大，则收缩可以缩短训练时间。但是，如果我们松散地解决优化问题(例如，通过使用大的停止公差)，不使用收缩的代码可能要快得多。
NuSVC/OneClassSVM/NuSVR中的参数nu近似训练误差和支持向量的分数。
在SVC中，如果数据是不平衡的(例如，许多正类和少量类)，设置 class_weight='balanced'和/或尝试不同的惩罚参数C。
底层实现的随机性：SVC和NuSVC的底层实现只使用随机数生成器来打乱数据顺序以进行概率估计(当probability设置为True时)。这种随机性可以用random_state参数来控制。如果probability被设为False，这些估计器就不是随机的，random_state对结果没有影响。底层OneClassSVM的实现类似于SVC和NuSVC的实现。由于没有为OneClassSVM提供概率估计，所以它不是随机的。

底层LinearSVC实现使用一个随机数生成器来选择特征，当拟合一个双坐标下降的模型时(dual 设置为 True)。因此，对于相同的输入数据有稍微不同的结果也是常见的。如果发生这种情况，请尝试使用较小的tol参数。这种随机性也可以通过random_state参数来控制。当dual设置为False时，LinearSVC的底层实现不是随机的，而且random_state对结果没有影响。

使用通过LinearSVC(loss='l2', penalty='l1', dual=False)使用L1正则化得到一个稀疏解，即有一部分特征权重不是0，并且对决策函数有贡献。增加C将生成一个更复杂的模型(更多的特征被选择)。可以使用l1_min_c去计算C值，这个C值会产生一个'null'模型(所有的权重都是0)。

1.4.6 核函数

核函数可以是以下任意一个：

线性核(linear):
多项式核(polynomial): , 其中是有参数degree指定, 是由coef0指定。
径向基核rbf: , 其中是有参数gamma指定，必须大于0。
sigmoid核：，其中是由参数coef0指定。

参数kernel 能够指定不同的核：

>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'

1.4.6.1 RBF核的参数

当使用径向基(RBF)核训练支持向量机时，必须考虑两个参数： C 和 gamma。参数C，是所有支持向量机核共有参数，决策面简单时，能够将分类错误的训练样本改变。一个低的C能够使决策面平滑，与此同时，一个高的C旨在能够正确类所有训练样本。gamma定义了单个训练样本有多大的影响力。一个大的gamma，其附近的其他样本一定会被影响到。

正确选择C和gamma是支持向量机性能的关键。建议使用sklearn.model_selection.GridSearchCV 与 C和gamma以指数间隔来选取一个好的数值。

示例：

RBF-SVM参数
非线性SVM

1.4.6.2 自定义核

你可以定义自己的核，可以通过给一个 python 函数作为核，或者通过计算一个Gram矩阵。

带有自定义内核的分类器的行为方式与任何其他分类器相同，以下除外：

support_vectors_现在是为空的，只有支持向量的索引存储在支持 support_中。
fit()方法中的第一个参数的引用(不是一个副本)为了未来的引用会被储存起来。如果那个数组在fit() 和 predict()之间的操作过程中被改变了，你将得到意料之外的结果。

1.4.6.2.1 使用Python函数作为核

你可以使用自己的核，通过传递给参数kernel一个函数。

你的函数核必须接受两个矩阵参数，形状分别是 (n_samples_1, n_features),和(n_samples_2, n_features)，并且返回的矩阵的形状是 (n_samples_1, n_samples_2)。

下面的代码定义了一个线性核，并且创建一个使用这个核的分类器实例：

>>> import numpy as np
>>> from sklearn import svm
>>> def my_kernel(X, Y):
...     return np.dot(X, Y.T)
...
>>> clf = svm.SVC(kernel=my_kernel)

示例
使用自定义核的支持向量机

1.4.6.2.2 使用Gram矩阵

你可以通过使用kernel='precomputed'来预先计算核。然后给fit()和predict()方法传递Gram矩阵而不是X。必须提供所有训练向量和测试向量之间的核值：

>>> import numpy as np
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import svm
>>> X, y = make_classification(n_samples=10, random_state=0)
>>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0)
>>> clf = svm.SVC(kernel='precomputed')
>>> # 线性核计算
>>> gram_train = np.dot(X_train, X_train.T)
>>> clf.fit(gram_train, y_train)
SVC(kernel='precomputed')
>>> # 在训练样本上做预测
>>> gram_test = np.dot(X_test, X_train.T)
>>> clf.predict(gram_test)
array([0, 1, 0])

1.4.7 数学公式

支持向量机在高维或无限维空间中构造超平面或超平面集，可用于分类、回归或其他任务。从直觉上看，一个好的分离的实现方案是, 超平面距离训练数据中任意一类的的样本的距离达到最大(也被称为函数间距)，因为通常来讲，间距越大，分类器的泛化误差就越小。下图显示了一个线性可分问题的决策函数，边界有三个样本，称为“支持向量”(“support vectors”)：

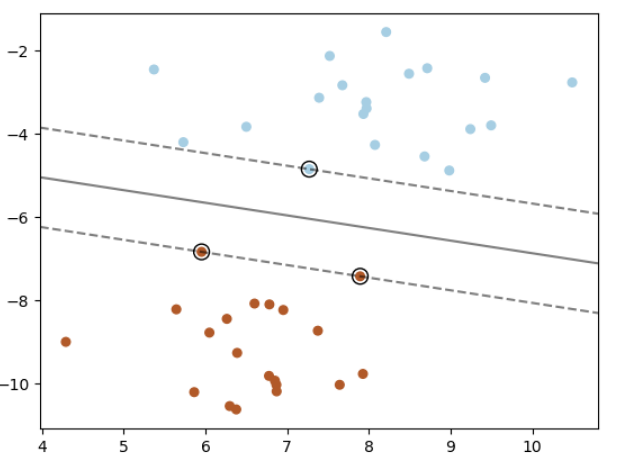通常，当问题不是线性可分时，支持向量是边界内的样本。

我们推荐[13]和[14]作为支持向量机的理论和实际应用的良好参考。

1.4.7.1 SVC

给定训练向量， =1, ..., n, 在两个类中，和一个向量，我们的目标是找到和对于给定的预测对大多数样本判断正确。

SVC主要能解决以下问题：

直觉上讲，我们要最大化间距(margin)(等价于最小化)，同时对于分类错误的样本或者在间距边界内部的样本会招致惩罚。理想情况下，对于所有样本来说的值都应该1，这会是一个完美的预测。但是问题通常并不总是与超平面完全分离，所以我们允许一些样本离它们正确的边缘边界有一个距离。惩罚项C控制着这个惩罚的强度，因此，作为一个正则化参数的倒数(见下面的注释)。

对原始问题的对偶问题是：

其中是一个全1的向量，是一个 x 的半正定矩阵， , 其中是内核。称为对偶系数，它们的上界是。这种对偶形示强调了这样一个事实，即训练向量可通过核函数ϕ隐式映射到一个更高(可能无限)维的空间：参见内核技巧。

一旦优化问题得到解决，给对于给定样本的决策函数的输出将变成：

预测的类对应于它的符号。我们只需要在支持向量(即位于边缘范围内的样本)上求和，因为对于其他样本，对偶系数为零。

可以通过以下属性访问这些参数： dual_coef_可以访问， support_vectors_可以访问支持向量intercept_可以访问截距项。

注意：

从libsvm和 liblinear 导出的支持向量机模型使用C作为正则化参数，而大多数其他估计器使用alpha。两个模型正则化量之间的严谨等价取决于模型所优化的特定的目标函数。比如：当所使用的估计器是sklearn.linemodel.Ridge回归时, 它们之间的关系是：

1.4.7.2 LinearSVC

原始问题可以等价地表示为：

其中，我们用到了合页损失 (hinge loss)。这是LinearSVC直接优化的形式，但与对偶形式不同的是，这种形式不涉及样本之间的内积，因此不能应用著名的内核技巧。这就是为什么LinearSVC只支持线性核(ϕ是标识函数)的原因。

1.4.7.3 NuSVC

-SVC公式[15]是C-SVC的重新参数化，因此在数学上是等价的。

我们引入了一个新的参数(来代替C)来控制支持向量的数目和边际误差：∈(0，1)是

我们引入了一个新的参数ν(而不是C)来控制支持向量和边缘误差的数目：ν是边际误差分数的上界和支持向量分数的下界。边际误差对应于位于边际边界错误一侧的样本：它要么被错误分类，要么被正确地分类，但不位于边际之外。

1.4.7.4 SVR

给定训练向量, =1, ...,n, 并且向量，能够解决以下主要问题：

在这里，我们惩罚的样本是那些预测值偏离他们真实目标至少的样本。这些样本的惩罚是通过或者，这取决于他们的预测值是在ε上方还是下方。

对偶问题是：

其中是所有为1的向量，是一个 x 的半正定矩阵，是核，这里，训练向量通过函数ϕ隐式映射到一个更高(可能无限)的维空间。

它的预测是：

可以通过下面的属性访问这些参数：dual_coef_能够访问不同的, support_vectors_可以访问支持向量， intercept_可以访问截距项。

1.4.7.5 LinearSVR

原始问题可以等价地表述为：

这里我们使用了epsilon-insensitive损失, 即小于ε的误差被忽略了。这是LinearSVR直接优化的方式。

1.4.8 实现细节

在内部，我们使用 libsvm [12] 和 liblinear [11]来处理所有的计算。这些库使用C和Cython包装。有关所使用算法的实现和详细信息，请参阅各自的论文。

参考：

[9] Platt “Probabilistic outputs for SVMs and comparisons to regularized likelihood methods”.

[10] Wu, Lin and Weng, “Probability estimates for multi-class classification by pairwise coupling”, JMLR 5:975-1005, 2004.

11(1, 2) Fan, Rong-En, et al., “LIBLINEAR: A library for large linear classification.”, Journal of machine learning research 9.Aug (2008): 1871-1874.

12(1,2) Chang and Lin, LIBSVM: A Library for Support Vector Machines.

[13] Bishop, Pattern recognition and machine learning, chapter 7 Sparse Kernel Machines

[14] “A Tutorial on Support Vector Regression”, Alex J. Smola, Bernhard Schölkopf - Statistics and Computing archive Volume 14 Issue 3, August 2004, p. 199-222.

[15] Schölkopf et. al New Support Vector Algorithms

[16] Crammer and Singer On the Algorithmic Implementation ofMulticlass Kernel-based Vector Machines, JMLR 2001.