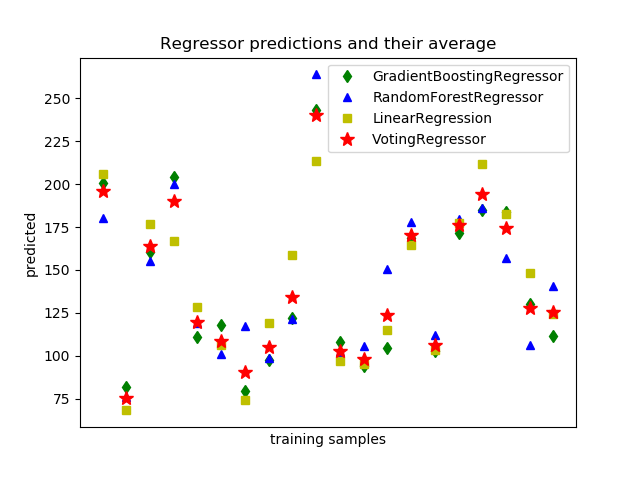
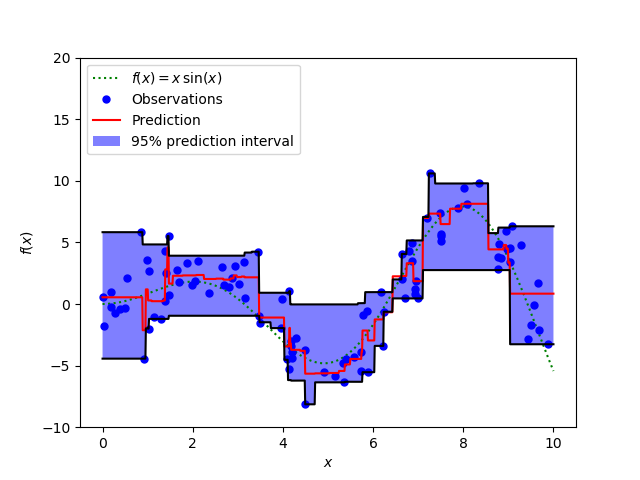
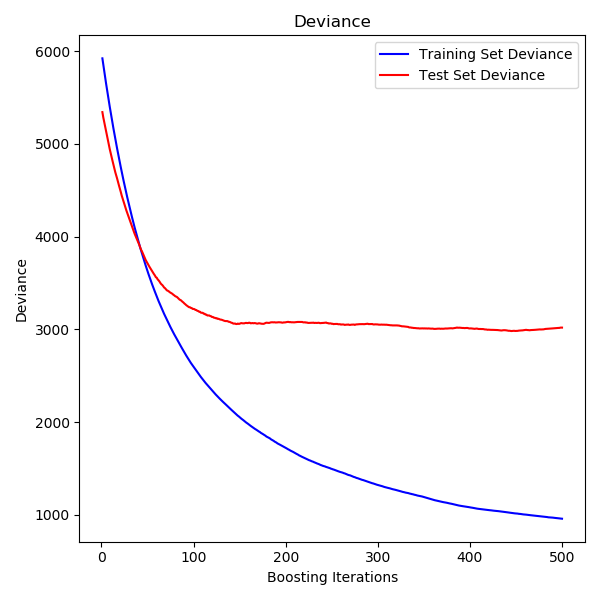
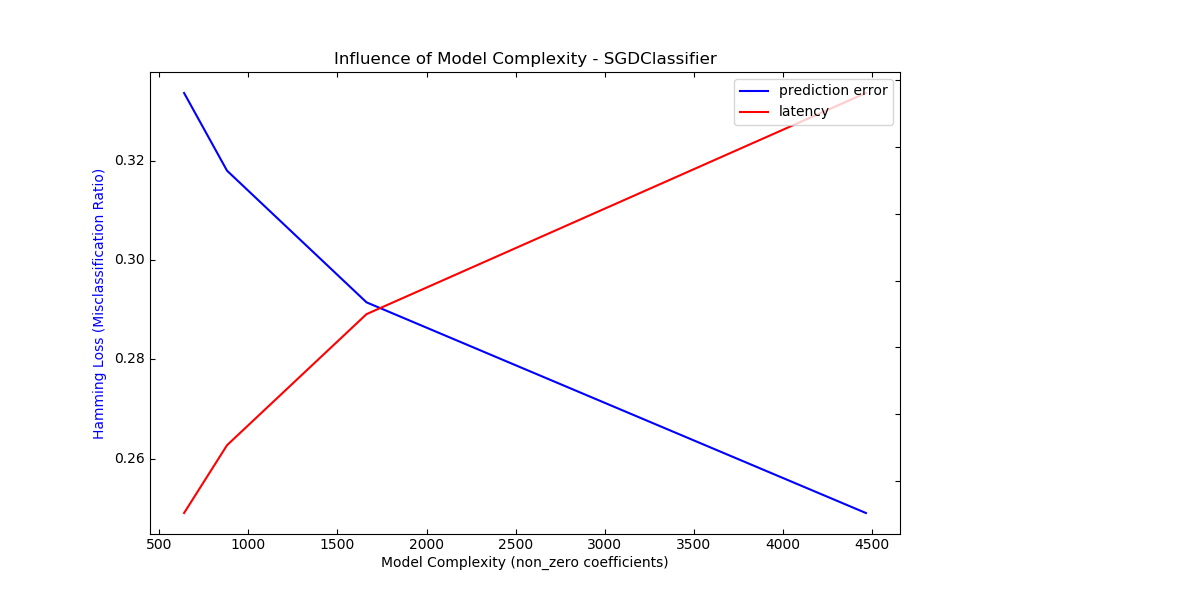
sklearn.ensemble.GradientBoostingRegressor¶
class sklearn.ensemble.GradientBoostingRegressor(*, loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort='deprecated', validation_fraction=0.1, n_iter_no_change=None, tol=0.0001, ccp_alpha=0.0)
回归的梯度增强。
GB采用正向阶段的方式建立加性模型;它允许优化任意可微的损失函数。在每一阶段,根据给定损失函数的负梯度拟合一棵回归树。
在用户指南中阅读更多内容。
| 参数 | 说明 |
|---|---|
| loss | {‘ls’, ‘lad’, ‘huber’, ‘quantile’}, default=’ls’ 待优化的损失函数。ls指的是最小二乘回归。“lad”(最小绝对偏差)是一个高度稳健的损失函数,仅基于输入变量的顺序信息。“huber”是两者的结合。允许"quantile"回归(使用 alpha来指定分位数)。 |
| learning_rate | float, default=0.1 学习率通过 learning_rate缩小每棵树的贡献。learning_rate和n_estimators之间存在权衡。 |
| n_estimators | int, default=100 要执行的推进阶段的数量。梯度增强对过拟合具有较强的鲁棒性,因此大量的梯度增强通常能取得较好的效果。 |
| subsample | float, default=1.0 用于拟合单个基本学习者的样本比例。如果小于1.0,会导致随机梯度提升。 subsample与参数n_estimators交互。选择subsample < 1.0会导致方差的减少和偏差的增加。 |
| criterion | {‘friedman_mse’, ‘mse’, ‘mae’}, default=’friedman_mse’ 该函数用来测量分割的质量。支持的标准是' friedman_mse ',即由Friedman提出的具有改进分数的均方误差, mse的平均平方误差,和' mae '的平均绝对误差。默认值' friedman_mse '通常是最好的,因为在某些情况下它可以提供更好的近似值。版本0.18中的新功能 |
| min_samples_leaf | 分割一个内部节点所需的最小样本数: - 如果为int,则认为 min_samples_leaf是最小值。- 如果为float, min_samples_leaf则为分数, 是每个节点的最小样本数。ceil(min_samples_leaf * n_samples)在版本0.18中更改:添加了分数的浮点值。 |
| min_samples_split | int or float, default=2 一个叶节点上所需的最小样本数。只有当它在每个左右分支中都留下至少 min_samples_leaf训练样本时,任何深度的分割点才会被考虑。这可能会产生平滑模型的效果,特别是在回归中。- 如果为int,则认为 min_samples_split是最小值。- 如果为float, min_samples_split则为分数, 是每个拆分的最小样本数。ceil(min_samples_split * n_samples)在版本0.18中更改:添加了分数的浮点值。 |
| min_weight_fraction_leaf | float, default=0.0 一个叶节点上所需的(所有输入样本的)总权重的最小加权分数。当不提供 sample_weight时,样本的重量相等。 |
| max_depth | int, default=3 单个回归估计量的最大深度。最大深度限制了树中的节点数。优化此参数以获得最佳性能;最佳值取决于输入变量的相互作用。 |
| min_impurity_decrease | float, default=0.0 如果节点分裂会导致杂质的减少大于或等于该值,则该节点将被分裂。 加权减少杂质的方程式如下: N_t / N * (impurity - N_t_R / N_t * right_impurity - N_t_L / N_t * left_impurity)其中, N是样本总数,N_t是当前节点上N_t_L的样本数,是左子节点中的样本N_t_R数,是右子节点中的样本数。N,N_t,N_t_R并且N_t_L都指的是加权和,如果sample_weight获得通过。版本0.19中的新功能。 |
| min_impurity_split | float, default=None 树提升提前停止的阈值。如果节点的杂质高于阈值,则该节点将分裂,否则为叶。 - 从版本0.19 min_impurity_split开始不推荐使用:在版本0.19中不再推荐使用 min_impurity_decrease。的默认值 min_impurity_split在0.23中从1e-7更改为0,并将在0.25中删除。使用min_impurity_decrease代替。 |
| init | estimator or ‘zero’, default=None 用于计算初始预测的估计对象。 init必须提供fit和predict_proba。如果为“零”,初始的原始预测被设置为零。默认情况下使用一个DummyEstimator,用于预测平均目标值(对于loss= 'ls')或其他损失的分位数。 |
| random_state | int, RandomState, default=None 控制每个增强迭代器上的树估计器随机种子。此外,它还可以在每次拆分时控制特性的随机排列(更多细节请参见注释)。如果 n_iter_no_change不是None,它还控制训练数据的随机分割以获得验证集。在多个函数调用之间传递可重复输出的int。有关更多详细信息,请参见Glossary。 |
| max_features | {‘auto’, ‘sqrt’, ‘log2’}, int or float, default=None 寻找最佳分割时要考虑的功能数量: - 如果为int,则 max_features在每个分割处考虑特征。- 如果为float, max_features则为小数,并 在每次拆分时考虑要素。- 如果为auto,则为 max_features=sqrt(n_features)。- 如果是sqrt,则 max_features=sqrt(n_features)。- 如果为log2,则为 max_features=log2(n_features)。- 如果为None,则 max_features=n_features。注意:直到找到至少一个有效的节点样本分区,分割的搜索才会停止,即使它需要有效检查多于 max_features个数的要素也是如此。 |
| alpha | float, default=0.9 huber损失函数的分位数和分位数损失函数。仅当 loss='huber'或loss='quantile'时 |
| verbose | int, default=0 启用详细输出。如果是1,那么它会在一段时间内打印进度和性能(树越多,频率越低)。如果大于1,则输出每棵树的进度和性能。 |
| max_leaf_nodes | int, default=None 以最佳优先的方式使用 max_leaf_nodes来种植树。最佳节点定义为杂质的相对减少。如果没有,则叶节点数没有限制。 |
| warm_start | bool, default=False 当设置为True时,重用前面调用的解决方案来适应并向集成添加更多的评估器,否则,只会拟合完整的新森林。有关更多详细信息,请参见Glossary。 |
| presort | deprecated, default=’deprecated’ 此参数不建议使用,将在v0.24中删除。 自版本0.22以来已弃用。 |
| validation_fraction | float, default=0.1 为提前停止而预留作为验证集的训练数据的比例。必须在0和1之间。仅在 n_iter_no_change被设置为整数时使用。0.20版中的新功能。 |
| n_iter_no_change | int, default=Nonen_iter_no_change用于决定在验证分数没有提高时是否使用早期停止来终止训练。默认情况下,它被设置为None来禁用提前停止。如果设置为一个数字,它将把训练数据的validation_fraction大小放在一边作为验证,并在之前所有的n_iter_no_change迭代次数中验证分数没有提高时终止训练。分裂是分层的。0.20版中的新功能。 |
| tol | float, default=1e-4 提前停止的的容忍度。当 n_iter_no_change迭代器(如果设置为一个数字)对tol的损失不再增加时,训练停止。0.20版中的新功能。 |
| ccp_alpha | non-negative float, default=0.0 复杂度参数用于最小代价复杂度剪枝。将选择代价复杂度最大且小于ccp_alpha的子树。默认情况下,不执行修剪。 有关更多详细信息,请参见Minimal Cost-Complexity Pruning。 0.22版中的新功能。 |
| 属性 | 说明 |
|---|---|
| feature_importances_ | ndarray of shape (n_features,) 基于杂质的特性重要性。 |
| oob_improvement_ | ndarray of shape (n_estimators,) 相对于之前的迭代,袋外样本损失(=偏差)的改进。 oob_improvement_[0]是init估计器的第一阶段损失的改进。仅当subsample < 1.0时可用。 |
| train_score_ | ndarray of shape (n_estimators,) 第 i个得分train_score_[i]是模型在第i次迭代时对袋装样本的偏差度(= loss)。如果subsample== 1,这便是训练数据上的偏差。 |
| loss_ | LossFunction 具体的LossFunction对象。 |
| init_ | estimator 提供最初预测的估计器。通过 init参数或loss.init_estimator设置。 |
| estimators_ | ndarray of DecisionTreeRegressor of shape (n_estimators, 1) 拟合的子估计器的集合 |
| classes_ | ndarray of shape (n_classes,) 类标签。 |
| n_features_ | int 数据的特征数。 |
| max_features_ | intmax_features的推断值。 |
另见:
注意:
在每次分割时,特性总是随机地进行分配。因此,即使在相同的训练数据和max_features=n_features的情况下,如果搜索最佳分割时列举的几个分割对准则的改进相同,那么找到的最佳分割也会有所不同。为了在拟合过程中获得确定性行为,必须修复random_state。
参考文献
J. Friedman, Greedy Function Approximation: A Gradient Boosting Machine, The Annals of Statistics, Vol. 29, No. 5, 2001.
10. Friedman, Stochastic Gradient Boosting, 1999
T. Hastie, R. Tibshirani and J. Friedman. Elements of Statistical Learning Ed. 2, Springer, 2009.
实例
>>> from sklearn.datasets import make_regression
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.model_selection import train_test_split
>>> X, y = make_regression(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> reg = GradientBoostingRegressor(random_state=0)
>>> reg.fit(X_train, y_train)
GradientBoostingRegressor(random_state=0)
>>> reg.predict(X_test[1:2])
array([-61...])
>>> reg.score(X_test, y_test)
0.4...
方法
| 方法 | 说明 |
|---|---|
apply(X) |
将森林中的树应用于X,返回叶子索引。 |
fit(X, y[, sample_weight, monitor]) |
拟合gradient boosting模型。 |
get_params([deep]) |
获取此估计器的参数。 |
predict(X) |
预测回归目标X。 |
score(X, y[, sample_weight]) |
返回预测的决定系数R^2。 |
set_params(**params) |
设置此估算器的参数。 |
staged_predict(X) |
预测X在每个阶段的回归目标。 |
__init__(*, loss='ls', learning_rate=0.1, n_estimators=100, subsample=1.0, criterion='friedman_mse', min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, alpha=0.9, verbose=0, max_leaf_nodes=None, warm_start=False, presort='deprecated', validation_fraction=0.1, n_iter_no_change=None, tol=0.0001, ccp_alpha=0.0)
初始化self。有关准确的签名,请参见help(type(self))。
apply(X)
将森林中的树应用于X,返回叶子索引。
0.17版本新功能
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 输入样本。在内部,它的 dtype将被转换为dtype=np.float32。如果提供了一个稀疏矩阵,它将被转换为一个csr_matrix。 |
| 返回值 | 说明 |
|---|---|
| X_leaves | ndarray of shape (n_samples, n_estimators) 对于X中的每个数据点x和森林中的每棵树,返回x最终所在的叶子的索引。 |
property feature_importances_
基于杂质的功能的重要性。
越高,功能越重要。特征的重要性计算为该特征带来的标准的(标准化)总缩减。这也被称为基尼重要性。
警告:基于杂质的特征重要性可能会误导高基数特征(许多唯一值)。另见 sklearn.inspection.permutation_importance。
| 返回值 | 说明 |
|---|---|
| feature_importances_ | ndarray of shape (n_features,) 除非所有树都是仅由根节点组成的单节点树,否则此数组的值总计为1,在这种情况下,它将是零数组。 |
fit(X, y, sample_weight=None, monitor=None)
拟合gradient boosting模型。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 输入样本。在内部,它将被转换为 dtype=np.float32。以及是否将稀疏矩阵提供给稀疏csr_matrix。 |
| y | array-like of shape (n_samples, ) 目标值(分类中的字符串或整数,回归中的实数)分类时,标签必须与类对应。 |
| sample_weight | array-like of shape (n_samples,), default=None 样本权重。如果没有,那么样本的权重相等。当在每个节点中搜索分割时,将忽略创建具有净零权值或负权值的子节点的分割。在分类的情况下,如果分割会导致任何一个类在任一子节点中具有负权值,那么分割也将被忽略。 |
| monitor | callable, default=None 使用当前迭代器下的对估计器的引用和 _fit_stages的局部变量作为可调用的关键字参数callable(i、self、locals()),在每次迭代之后调用监视器。如果callable返回True,拟合过程将停止。该监视器可用于各种各样的情景,如计算拉出的估计、提前停止、模型内省和快照。 |
| 返回值 | 说明 |
|---|---|
| self | object |
get_params(deep=True)
获取此估计器的参数。
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为True,则将返回此估算器和作为估算器的所包含子对象的参数。 |
| 返回值 | 说明 |
|---|---|
| params | mapping of string to any 参数名称与其值相对应。 |
predict(X)
预测回归目标X。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 输入样本。在内部,它将被转换为 dtype=np.float32。以及是否将稀疏矩阵提供给稀疏csr_matrix。 |
| 返回值 | 说明 |
|---|---|
| y | ndarray of shape (n_sample, ) 预测后的回归值。 |
score(X, y, sample_weight=None)
返回预测的决定系数R^2。
定义系数R^2为(1 - u/v),其中u为(y_true - y_pred) ** 2).sum()的残差平方和,v为(y_true - y_true.mean()) ** 2).sum()的平方和。最好的可能的分数是1.0,它可能是负的(因为模型可能会变的更糟)。一个常数模型总是预测y的期望值,而不考虑输入特征,得到的R^2得分为0.0。
注意
调用回归变量上的score时使用的R2 score使用0.23版本的multioutput='uniform_average'来保持与 r2_score的默认值一致。这影响了所有多输出回归的评分方法(除了 MultiOutputRegressor)
| 参数 | 说明 |
|---|---|
| X | array-like of shape (n_sample, n_features) 测试样品。对于某些估计器,这可能是一个预先计算的内核矩阵或一列通用对象,而不是 shape= (n_samples, n_samples_fitting),其中n_samples_fitting是用于拟合估计器的样本数量。 |
| y | array-like of shpe (n_sample, ) or (n_samples, n_outputs) X的值。 |
| sample_weight | array-like of shape (n_samples, ), default = None 样本权重。 |
| 返回值 | 说明 |
|---|---|
| score | float self.predict(X) 关于y的平均准确率。 |
set_params(**params)
设置该估计器的参数。
该方法适用于简单估计器和嵌套对象(如pipline)。后者具有形式为<component>_<parameter>的参数,这样就可以更新嵌套对象的每个组件。
| 参数 | 说明 |
|---|---|
| **params | dict 估计器参数 |
| 返回值 | 说明 |
|---|---|
| self | object 估计实例。 |
staged_predict(X)
返回X阶段性的预测。
该方法允许在每个阶段后进行监控(即在测试集上确定错误)。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 输入样本。在内部,它将被转换为 dtype=np.float32。以及是否将稀疏矩阵提供给稀疏csr_matrix。 |
| 产出 | 说明 |
|---|---|
| y | generator of ndarray of shape (n_samples, ) 预测后的回归值。 |