sklearn.covariance.LedoitWolf¶
class sklearn.covariance.LedoitWolf(*, store_precision=True, assume_centered=False, block_size=1000)
Ledoit-Wolf估计器
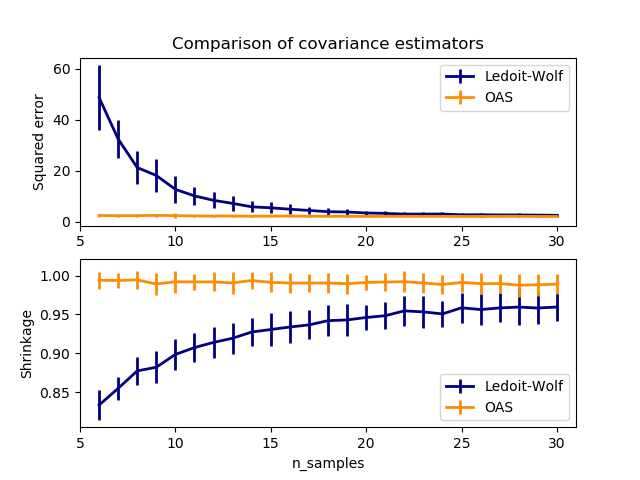
Ledoit-Wolf是一种特殊的收敛形式,其收缩系数是使用O. Ledoit和M. Wolf公式计算得出的,该公式在“A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices”中进行了描述,作者是Ledoit和Wolf,《多元分析杂志》,第88卷,第2期,2004年2月,第365-411页。
在用户指南中阅读更多内容。
| 参数 | 说明 |
|---|---|
| store_precision | bool, default=True 指定是否存储估计的精度。 |
| assume_centered | bool, default=False 如果为True,则在计算之前数据不会中心化。这在处理均值几乎为零但不完全为零的数据时很有用。如果为False(默认),则数据将在计算之前进行中心化。 |
| block_size | int, default=1000 在Ledoit-Wolf估计期间将协方差矩阵进行分块。这纯粹是内存优化,不会影响结果。 |
| 属性 | 说明 |
|---|---|
| covariance_ | ndarray of shape (n_features, n_features) 估计的协方差矩阵。 |
| location_ | ndarray of shape (n_features,) 估计位置,即估计平均值。 |
| precision_ | ndarray of shape (n_features, n_features) 估计的伪逆矩阵。(仅在store_precision为True时存储) |
| shrinkage_ | float 用于收缩估计中的凸组合系数。范围是[0,1]。 |
注
正则协方差为:
(1 - shrinkage) * cov + shrinkage * mu * np.identity(n_features)
其中mu = trace(cov)/ n_features,收敛率由Ledoit和Wolf公式给出(请参阅参考资料)
参考资料
“A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices”, Ledoit and Wolf, Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.
示例
>>> import numpy as np
>>> from sklearn.covariance import LedoitWolf
>>> real_cov = np.array([[.4, .2],
... [.2, .8]])
>>> np.random.seed(0)
>>> X = np.random.multivariate_normal(mean=[0, 0],
... cov=real_cov,
... size=50)
>>> cov = LedoitWolf().fit(X)
>>> cov.covariance_
array([[0.4406..., 0.1616...],
[0.1616..., 0.8022...]])
>>> cov.location_
array([ 0.0595... , -0.0075...])
方法
| 方法 | 说明 |
|---|---|
error_norm(self, comp_cov[, norm, scaling, …]) |
计算两个协方差估计量之间的均方误差。 |
fit(self, X[, y]) |
根据给定的训练数据和参数,拟合Ledoit-Wolf收敛协方差模型。 |
get_params(self[, deep]) |
获取此估算器的参数。 |
get_precision(self) |
获取精确度矩阵 |
mahalanobis(self, X) |
计算给定观测值的平方马氏距离。 |
score(self, X_test[, y]) |
使用self.covariance_计算高斯数据集的对数似然值,作为其协方差矩阵的估计量。 |
set_params(self, **params) |
设置此估算器的参数。 |
__init__(self, *, store_precision=True, assume_centered=False, block_size=1000)
初始化self. 请参阅help(type(self))以获得准确的说明。
error_norm(self, comp_cov, norm='frobenius', scaling=True, squared=True)
[源码]
计算两个协方差估计量之间的均方误差。(在Frobenius规范的意义上)。
| 参数 | 说明 |
|---|---|
| comp_cov | array-like of shape (n_features, n_features) 要比较的协方差。 |
| norm | {“frobenius”, “spectral”}, default=”frobenius” 用于计算误差的规范类型,可用的误差类型: - ‘frobenius’ (default): - ‘spectral’: 这里的A是 (comp_cov - self.covariance_)的误差 |
| scaling | bool, default=True 如果为True(默认),则平方误差范数除以n_features。如果为False,则不会重新调整平方误差范数。 |
| squared | bool, default=True 是计算平方误差范数还是误差范数。如果为True(默认),则返回平方误差范数。如果为False,则返回误差范数。 |
| 返回值 | 说明 |
|---|---|
| result | floatself和comp_cov协方差估计量之间的均方误差(按照Frobenius范式的含义) 。 |
fit(self,X,y = None )
根据给定的训练数据和参数,拟合Ledoit-Wolf收敛协方差模型。
| 参数 | 说明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 训练数据,其中 n_samples是样本数量,n_features是特征数量。 |
| y | Ignored 未使用,出于API一致性目的而存在。 |
| 返回值 | 说明 |
|---|---|
| self | object |
get_params(self, deep=True)
获取此估计器的参数。
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为True,则将返回此估算器与其所包含子对象的参数。 |
| 返回值 | 说明 |
|---|---|
| params | mapping of string to any 参数名称映射到其值。 |
get_precision(self)
获取精确度矩阵。
| 返回值 | 说明 |
|---|---|
| precision_ | array-like of shape (n_features, n_features) 与当前协方差对象关联的精度矩阵。 |
mahalanobis(self, X)
计算给定观测值的平方马氏距离。
| 参数 | 说明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 观测值,用来计算马氏距离。假定观测值与fit中使用的数据来自相同的分布。 |
| 返回值 | 说明 |
|---|---|
| dist | ndarray of shape (n_samples,) 观测值的平方马氏距离。 |
score(self, X_test, y=None)
使用self.covariance_作为协方差矩阵的估计值来计算高斯数据集的对数似然 。
| 参数 | 说明 |
|---|---|
| X_test | array-like of shape (n_samples, n_features) 计算似然性的测试数据集,其中n_samples是样本数,n_features是特征数。假定X_test与拟合(包括中心化)使用的数据来自相同的分布。 |
| y | Ignored 未使用,出于API一致性目的而存在。 |
| 返回值 | 说明 |
|---|---|
| res | float 数据集以 self.covariance_作为其协方差矩阵的估计量的似然性。 |
set_params(self, **params)
设置此估计器的参数。
该方法适用于简单的估计器以及嵌套对象(例如管道)。后者具有形式参数<component>__<parameter>以便可以更新嵌套对象的每个组件。
| 参数 | 说明 |
|---|---|
| **params | dict 估算器参数。 |
| 返回值 | 参数 |
|---|---|
| self | object 估算器对象。 |