sklearn.linear_model.TweedieRegressor¶
class sklearn.linear_model.TweedieRegressor(*, power=0.0, alpha=1.0, fit_intercept=True, link='auto', max_iter=100, tol=0.0001, warm_start=False, verbose=0)
具有Tweedie分布的广义线性模型。
此估计器可用于根据power参数确定不同的GLM ,从而确定基础分布。
在用户指南中阅读更多内容。
| 参数 | 说明 |
|---|---|
| power | float, default=0 power根据下表确定基础目标分布: 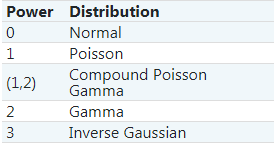 对于 0 < power < 1,不存在分布。 |
| alpha | float, default=1 该常数乘以惩罚项,从而确定正则化强度。 alpha = 0等同于未惩罚的GLM。在这种情况下,设计矩阵X必须具有全列秩(无共线性)。 |
| link | {‘auto’, ‘identity’, ‘log’}, default=’auto’ GLM的链接函数,即从线性预测模型 X @ coeff + intercept到预测值y_pred的映射 。选项“auto”根据所选族设置link,如下所示:- ‘identity’ 对应正态分布 - ‘log’ 对应泊松,伽玛和高斯逆分布 |
| fit_intercept | bool, default=True 是否将常数(即偏置或截距)添加到线性预测模型(X @ coef +截距)。 |
| max_iter | int, default=100 求解器的最大迭代次数。 |
| tol | float, default=1e-4 停止标准。对于lbfgs求解器,当 max{g_j,j = 1, ..., d} <= tol,其中g_j为目标函数的梯度(导数)的第j个分量,迭代将停止。 |
| warm_start | bool, default=False 如果设置为 True,重用前面调用的解决方案进行fit,作为coef_和intercept_的初始化。 |
| verbose | int, default=0 对于lbfgs求解器,请将verbose设置为代表详细程度的任何正数。 |
| 属性 | 说明 |
|---|---|
| coef_ | array of shape (n_features,) GLM中线性预测模型( X @ coef_ + intercept_)的估计系数。 |
| intercept_ | float 已添加到线性预测变量中的截距(又称偏置)。 |
| n_iter_ | int 求解器中使用的实际迭代数。 |
方法
| 方法 | 说明 |
|---|---|
fit(X, y[, sample_weight]) |
拟合广义线性模型。 |
get_params([deep]) |
获取此估计器的参数。 |
predict(X) |
利用GLM与特征矩阵X进行预测。 |
score(X, y[, sample_weight]) |
计算D ^ 2,说明偏差百分比。 |
set_params(**params) |
设置此估计器的参数。 |
__init__(*, power=0.0, alpha=1.0, fit_intercept=True, link='auto', max_iter=100, tol=0.0001, warm_start=False, verbose=0)
初始化self, 请参阅help(type(self))以获得准确的说明。
fit(X, y, sample_weight=None)
[源码]
拟合广义线性模型。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 训练数据。 |
| y | array-like of shape (n_samples,) 目标值。 |
| sample_weight | array-like of shape (n_samples,), default=None 样本权重 |
| 返回值 | 说明 |
|---|---|
| self | returns an instance of self. |
get_params(deep=True)
[源码]
获取此估计器的参数。
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为True,则将返回此估算器和所包含子对象的参数。 |
| 返回值 | 说明 |
|---|---|
| params | mapping of string to any 参数名称映射到其值。 |
predict(X)
[源码]
使用GLM与特征矩阵X进行预测。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 样本数据 |
| 返回值 | 说明 |
|---|---|
| y_pred | array of shape (n_samples,) 返回预测值。 |
score(X, y, sample_weight=None)
[源码]
计算D ^ 2,说明偏差百分比。
D ^ 2是确定系数R ^ 2的推广。R ^ 2使用平方误差,D ^ 2使用偏差。请注意,对于family='normal',这两个是相等的。
D ^ 2定义为, 是零偏差,即仅具有截距的模型的偏差,对应于 。均值由sample_weight取平均值。最佳可能得分为1.0,并且可能为负(因为该模型可能会更差)。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 测试样本。 |
| y | array-like of shape (n_samples,) 目标的真实值。 |
| sample_weight | array-like of shape (n_samples,), default=None 样本权重。 |
| 返回值 | 说明 |
|---|---|
| score | float 预测值与真实值的D^2。 |
set_params(**params)
[源码]
设置此估计器的参数。
该方法适用于简单的估计器以及嵌套对象(例如管道)。后者具有形式为 <component>__<parameter>的参数,这样就可以更新嵌套对象的每个组件。
| 参数 | 说明 |
|---|---|
| **params | dict 估计器参数。 |
| 返回值 | 说明 |
|---|---|
| self | object 估计器实例。 |