sklearn.linear_model.TheilSenRegressor¶
class sklearn.linear_model.TheilSenRegressor(*, fit_intercept=True, copy_X=True, max_subpopulation=10000.0, n_subsamples=None, max_iter=300, tol=0.001, random_state=None, n_jobs=None, verbose=False)
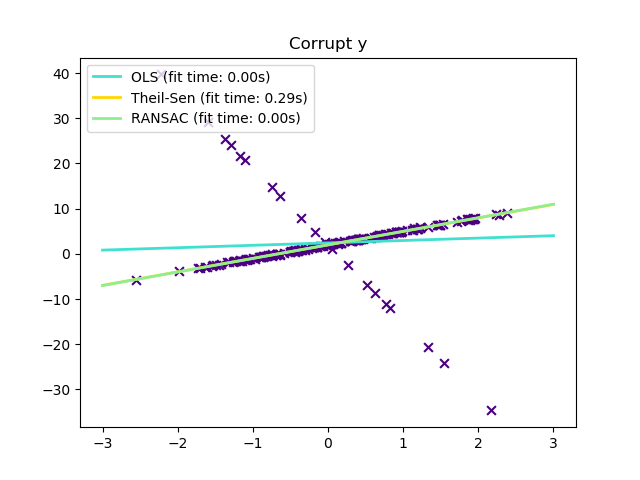
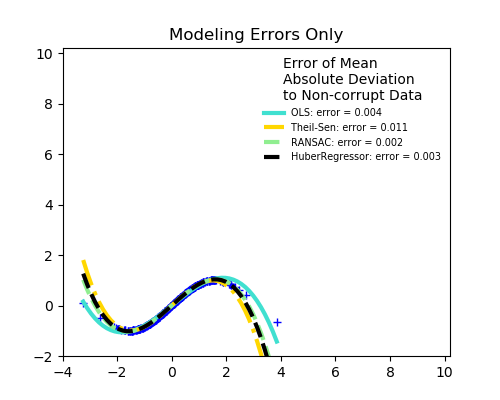
Theil-Sen估计器:稳健的多元回归模型。
该算法计算X中样本大小为n_subsample的子集的最小二乘解。在特征数和样本数之间的任意n_subsamples值都可以得到一种鲁棒性和效率之间折衷的估计器。因为最小二乘解的个数是“n_samples select n_subsamples”,所以它可以非常大,因此可以使用max_subpopulation进行限制。如果达到此限制,则随机选择子集。在最后一步中,将计算所有最小二乘解的空间中位数(或L1中位数)。
在用户指南中阅读更多内容。
| 参数 | 说明 |
|---|---|
| fit_intercept | boolean, optional, default True 是否计算此模型的截距。如果设置为false,则在计算中将不使用截距。 |
| copy_X | boolean, optional, default True 如果为True,将复制X;否则X可能会被覆盖。 |
| max_subpopulation | int, optional, default 1e4 利用‘n choose k’的集合进行计算,这里n是样本的数量,k是子样本的数量(至少是特征的数量),如果‘n choose k’大于max_subpopulation,只考虑给定最大规模的随机子总体。对于较小的问题,如果不更改n_subsamples,则此参数将确定内存使用情况和运行时间。 |
| n_subsamples | int, optional, default None 计算参数的样本数。至少是特征数量(如果fit_intercept = True,则为加1),并且样本的数量为最大值。数值越小,故障点越多,效率越低;数值越大,故障点越少,效率越高。如果为“无”,则采用最小数量的子样本,以实现最大的鲁棒性。如果将n_subsamples设置为n_samples,则Theil-Sen与最小二乘法相同。 |
| max_iter | int, optional, default 300 计算空间中位数的最大迭代次数。 |
| tol | float, optional, default 1.e-3 计算空间中位数时的容忍度。 |
| random_state | int, RandomState instance, default=None 随机数生成器实例,用于定义随机排列生成器的状态。通过传递一个整数实现多个函数调用传递可重复输出。见词汇表。 |
| n_jobs | int or None, optional (default=None) 交叉验证期间要使用的CPU数量。 除非上下文中设置了 joblib.parallel_backend参数,否则None表示1 。 -1表示使用所有处理器。有关更多详细信息,请参见词汇表。 |
| verbose | boolean, optional, default False 拟合模型时的详细模式。 |
| 属性 | 说明 |
|---|---|
| coef_ | array, shape = (n_features) 回归模型的系数(分布的中位数)。 |
| intercept_ | float 回归模型的估计截距。 |
| breakdown_ | float 近似故障点。 |
| n_iter_ | int 空间中位数所需的迭代次数。 |
| n_subpopulation_ | int “ n choose k”中考虑的组合数,其中n是样本数,k是子样本数。 |
参考
Theil-Sen Estimators in a Multiple Linear Regression Model, 2009 Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang http://home.olemiss.edu/~xdang/papers/MTSE.pdf
示例
>>> from sklearn.linear_model import TheilSenRegressor
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(
... n_samples=200, n_features=2, noise=4.0, random_state=0)
>>> reg = TheilSenRegressor(random_state=0).fit(X, y)
>>> reg.score(X, y)
0.9884...
>>> reg.predict(X[:1,])
array([-31.5871...])
方法
| 方法 | 说明 |
|---|---|
fit(X, y) |
拟合线性模型。 |
get_params([deep]) |
获取此估计器的参数。 |
predict(X) |
使用线性模型进行预测。 |
score(X, y[, sample_weight]) |
返回预测的确定系数R ^ 2。 |
set_params(**params) |
设置此估算器的参数。 |
__init__(*,fit_intercept = True,copy_X = True,max_subpopulation = 10000.0,n_subsamples = None,max_iter = 300,tol = 0.001,random_state = None,n_jobs = None,verbose = False )
初始化self, 请参阅help(type(self))以获得准确的说明。
fit(X,y )
[源码]
拟合线性模型。
| 参数 | 说明 |
|---|---|
| X | numpy array of shape [n_samples, n_features] 训练数据。 |
| y | numpy array of shape [n_samples] 目标值。 |
| 返回值 | 说明 |
|---|---|
| self | returns an instance of self. |
get_params(deep=True)
[源码]
获取此估计器的参数。
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为True,则将返回此估算器和所包含子对象的参数。 |
| 返回值 | 说明 |
|---|---|
| params | mapping of string to any 参数名称映射到其值。 |
predict(X)
[源码]
使用线性模型进行预测。
| 参数 | 说明 |
|---|---|
| X | array_like or sparse matrix, shape (n_samples, n_features) 样本数据 |
| 返回值 | 说明 |
|---|---|
| C | array, shape (n_samples,) 返回预测值。 |
score(X, y, sample_weight=None)
[源码]
返回预测的确定系数R ^ 2。
系数R ^ 2定义为(1- u / v),其中u是残差平方和((y_true-y_pred)** 2).sum(),而v是总平方和((y_true- y_true.mean())** 2).sum()。可能的最高得分为1.0,并且也可能为负(因为该模型可能会更差)。一个常数模型总是预测y的期望值,而不考虑输入特征,得到的R^2得分为0.0。
| 参数 | 说明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 测试样本。对于某些估计器,这可以是预先计算的内核矩阵或通用对象列表,形状为(n_samples,n_samples_fitted),其中n_samples_fitted是用于拟合估计器的样本数。 |
| y | array-like of shape (n_samples,) or (n_samples, n_outputs) X对应的真实值。 |
| sample_weight | array-like of shape (n_samples,), default=None 样本权重。 |
| 返回值 | 说明 |
|---|---|
| score | float 预测值与真实值的R^2。 |
注
调用回归器中的score时使用的R2分数,multioutput='uniform_average'从0.23版开始使用 ,与r2_score默认值保持一致。这会影响多输出回归的score方法( MultiOutputRegressor除外)。
set_params(**params)
[源码]
设置此估计器的参数。
该方法适用于简单的估计器以及嵌套对象(例如管道)。后者具有形式为 <component>__<parameter>的参数,这样就可以更新嵌套对象的每个组件。
| 参数 | 说明 |
|---|---|
| **params | dict 估计器参数。 |
| 返回值 | 说明 |
|---|---|
| self | object 估计器实例。 |