sklearn.linear_model.HuberRegressor¶
class sklearn.linear_model.HuberRegressor(*, epsilon=1.35, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)
对异常值具有鲁棒性的线性回归模型。
Huber回归器优化了|(y - X'w) / sigma| < epsilon的样本的平方损失和|(y - X'w) / sigma| > epsilon的样本的绝对损失,其中w和sigma是要优化的参数。参数sigma可确保如果y按一定的比例增大或减小,则无需重新缩放epsilon即可达到相同的鲁棒性。注意,这没有考虑X的不同特征可能具有不同尺度的事实。
这确保了损失函数不会受到异常值的严重影响,同时又不会完全忽略其影响。
在用户指南中阅读更多内容。
版本0.18中的新功能。
| 参数 | 说明 |
|---|---|
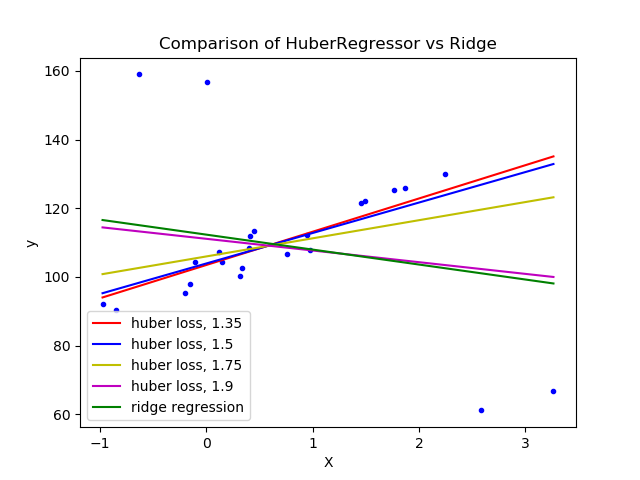
| epsilon | float, greater than 1.0, default 1.35 参数epsilon控制应分类为异常值的样本数。epsilon越小,对异常值的鲁棒性越强。 |
| max_iter | int, default 100scipy.optimize.minimize(method="L-BFGS-B")应该运行的最大迭代次数。 |
| alpha | float, default 0.0001 正则化参数。 |
| warm_start | bool, default False 如果必须重用先前使用的模型的存储属性,这是非常有用的。如果设置为False,则每次调用时系数将被重写。请参阅词汇表。 |
| fit_intercept | bool, default True 是否拟合截距。如果数据已经经过中心化,则可以将其设置为False。 |
| tol | float, default 1e-5 当 max{\proj g_i\i = 1, ..., n}<= tol时,迭代将停止, 其中pg_i是投影渐变的第i个分量。 |
| 属性 | 说明 |
|---|---|
| coef_ | array, shape (n_features,) 通过优化Huber损失获得的特征。 |
| intercept_ | float 偏置。 |
| scale_ | float 值将按 \y - X'w - c\比例缩小。 |
| n_iter_ | intscipy.optimize.minimize(method="L-BFGS-B")已运行的迭代次数 。*在0.20版中更改:*在SciPy <= 1.0.0中,lbfgs迭代次数可能超过 max_iter。n_iter_现在将报告最大的max_iter。 |
| outliers_ | array, shape (n_samples,) 设置为True的布尔掩码,其中样本被标识为离群值。 |
参考
1 Peter J. Huber, Elvezio M. Ronchetti, Robust Statistics Concomitant scale estimates, pg 172
2 Art B. Owen (2006), A robust hybrid of lasso and ridge regression. https://statweb.stanford.edu/~owen/reports/hhu.pdf
示例
>>> import numpy as np
>>> from sklearn.linear_model import HuberRegressor, LinearRegression
>>> from sklearn.datasets import make_regression
>>> rng = np.random.RandomState(0)
>>> X, y, coef = make_regression(
... n_samples=200, n_features=2, noise=4.0, coef=True, random_state=0)
>>> X[:4] = rng.uniform(10, 20, (4, 2))
>>> y[:4] = rng.uniform(10, 20, 4)
>>> huber = HuberRegressor().fit(X, y)
>>> huber.score(X, y)
-7.284...
>>> huber.predict(X[:1,])
array([806.7200...])
>>> linear = LinearRegression().fit(X, y)
>>> print("True coefficients:", coef)
True coefficients: [20.4923... 34.1698...]
>>> print("Huber coefficients:", huber.coef_)
Huber coefficients: [17.7906... 31.0106...]
>>> print("Linear Regression coefficients:", linear.coef_)
Linear Regression coefficients: [-1.9221... 7.0226...]
方法
| 方法 | 说明 |
|---|---|
fit(X, y[, sample_weight]) |
根据给定的训练数据拟合模型。 |
get_params([deep]) |
获取此估计器的参数。 |
predict(X) |
使用线性模型进行预测。 |
score(X, y[, sample_weight]) |
返回预测的确定系数R ^ 2。 |
set_params(**params) |
设置此估算器的参数。 |
__init__(*, epsilon=1.35, max_iter=100, alpha=0.0001, warm_start=False, fit_intercept=True, tol=1e-05)
初始化self, 请参阅help(type(self))以获得准确的说明。
fit(X, y, sample_weight=None)
[源码]
根据给定的训练数据拟合模型。
| 参数 | 说明 |
|---|---|
| X | array-like, shape [n_samples, n_features] 训练数据,其中n_samples是样本数量,n_features是特征数量。 |
| y | array-like, shape [n_samples] 对应X的目标向量。 |
| sample_weight | array-like, shape (n_samples,) 给每个样本的权重。 |
| 返回值 | 说明 |
|---|---|
| self | object |
get_params(deep=True)
[源码]
获取此估计器的参数。
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为True,则将返回此估算器和所包含子对象的参数。 |
| 返回值 | 说明 |
|---|---|
| params | mapping of string to any 参数名称映射到其值。 |
predict(X)
[源码]
使用线性模型进行预测。
| 参数 | 说明 |
|---|---|
| X | array_like or sparse matrix, shape (n_samples, n_features) 样本数据 |
| return_std | bool, default=False 是否返回后验预测的标准差。 |
| 返回值 | 说明 |
|---|---|
| C | array, shape (n_samples,) 返回预测值。 |
score(X, y, sample_weight=None)
[源码]
返回预测的确定系数R ^ 2。
系数R ^ 2定义为(1- u / v),其中u是残差平方和((y_true-y_pred)** 2).sum(),而v是总平方和((y_true- y_true.mean())** 2).sum()。可能的最高得分为1.0,并且也可能为负(因为该模型可能会更差)。一个常数模型总是预测y的期望值,而不考虑输入特征,得到的R^2得分为0.0。
| 参数 | 说明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 测试样本。对于某些估计器,这可以是预先计算的内核矩阵或通用对象列表,形状为(n_samples,n_samples_fitted),其中n_samples_fitted是用于拟合估计器的样本数。 |
| y | array-like of shape (n_samples,) or (n_samples, n_outputs) X对应的真实值。 |
| sample_weight | array-like of shape (n_samples,), default=None 样本权重。 |
| 返回值 | 说明 |
|---|---|
| score | float 预测值与真实值的R^2。 |
注
调用回归器中的score时使用的R2分数,multioutput='uniform_average'从0.23版开始使用 ,与r2_score默认值保持一致。这会影响多输出回归的score方法( MultiOutputRegressor除外)。
set_params(**params)
[源码]
设置此估计器的参数。
该方法适用于简单的估计器以及嵌套对象(例如管道)。后者具有形式为 <component>__<parameter>的参数,这样就可以更新嵌套对象的每个组件。
| 参数 | 说明 |
|---|---|
| **params | dict 估计器参数。 |
| 返回值 | 说明 |
|---|---|
| self | object 估计器实例。 |