sklearn.cluster.MiniBatchKMeans¶
class sklearn.cluster.MiniBatchKMeans(n_clusters=8, *, init='k-means++', max_iter=100, batch_size=100, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init=3, reassignment_ratio=0.01)
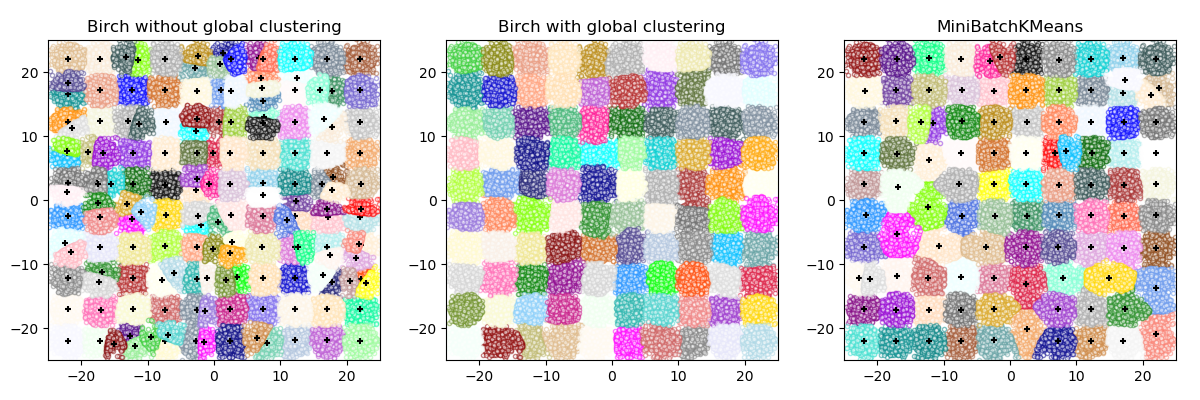
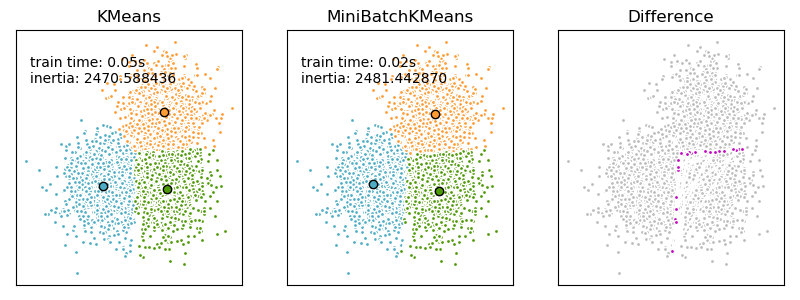
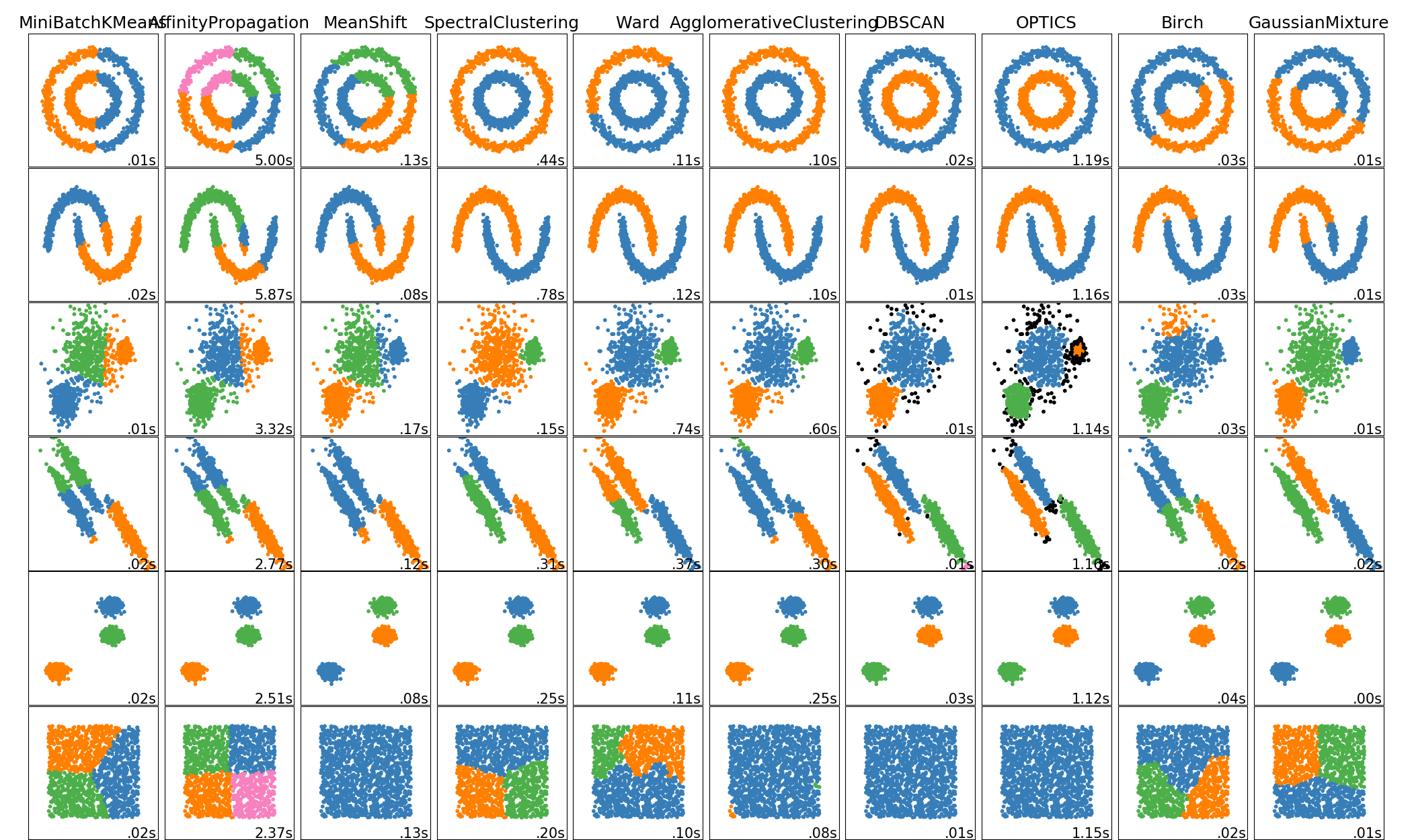
Mini-Batch K-Means聚类
在用户指南中阅读更多内容。
| 参数 | 方法 |
|---|---|
| n_clusters | int, default=8 要形成的簇数以及要生成的质心数。 |
| init | {‘k-means++’, ‘random’, ndarray, callable}, default=’k-means++’ 初始化方法 ‘k-means++’:明智地选择初始聚类中心进行k均值聚类,加快收敛速度.有关详细信息,请参阅k_init中的Notes部分。 ‘random’:从初始质心的数据中随机选择 n_clusters观测(行)。 如果一个ndarray被传递,它应该是形状的(n_clusters, n_features),并给出初始中心。 如果传递了一个可调用函数,它应该接受参数X、n_clusters和一个随机状态,并返回一个初始化。 |
| max_iter | int, default=300 相对容忍度与Frobenius范数, 连续两次迭代之间的聚类中心的差异声明收敛。不建议将其设置为 tol=0,因为由于舍入错误,可能永远不会声明收敛。用一个很小的数字代替。 |
| batch_size | int, default=100 小批次的大小 |
| verbose | int, default=0 详细模式 |
| compute_labels | bool, default=True 一旦小批优化在合适的情况下收敛,计算完整数据集的标签分配和inertia。 |
| random_state | int, RandomState instance, default=None 确定用于质心初始化的随机数生成。使用整数使随机性确定。见Glossary。 |
| tol | float, default=0.0 根据平均中心平方位置变化的平滑、方差归一化所测量的相对中心变化来控制早期停止。这种早期停止启发式方法更接近于算法的批处理变体,但在inertia启发式的基础上引起了较小的计算和内存开销。 |
| max_no_improvement | int, default=10 根据连续的小批数控制早期停止,这些小批次不会改善平滑的inertia。 若要禁用基于inertia的收敛检测,请将max_no_improvement设置为None。 |
| init_size | int, default=None 为加速初始化而随机抽样的样本数(有时以牺牲准确性为代价):唯一的算法是通过在数据的随机子集上运行批处理KMeans来初始化的。需要大于n_clusters。 如果为 None,init_size= 3 * batch_size。 |
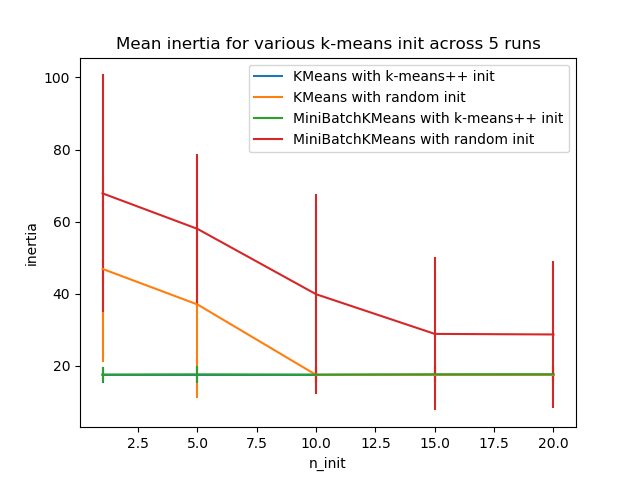
| n_init | int, default=3 尝试的随机初始化数。与KMeans相比,该算法只运行一次,使用inertia度量的 n_init初始化中的最佳值。 |
| reassignment_ratio | float, default=0.01 控制要重新分配的中心的最大计数数的分数。较高的值意味着低计数中心更容易重新分配,这意味着模型将需要更长的时间来收敛,但应该在更好的聚类中收敛。 |
| 参数 | 属性 |
|---|---|
| cluster_centers_ | ndarray of shape (n_clusters, n_features) 簇中心坐标 |
| labels_ | int 每个点的标签(如果计算标签设置为True)。 |
| inertia_ | float 与所选分区相关联的inertia准则的值(如果计算标签设置为True)。inertia被定义为样本到最近邻居的平方距离之和。 |
另见
基于劳埃德算法的聚类方法的经典实现。它在每次迭代时消耗整个输入数据集。
注
参见:https://www.eecs.tufts.edu/~dsculley/papers/fastkmeans.pdf
示例
>>> from sklearn.cluster import MiniBatchKMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [4, 2], [4, 0], [4, 4],
... [4, 5], [0, 1], [2, 2],
... [3, 2], [5, 5], [1, -1]])
>>> # manually fit on batches
>>> kmeans = MiniBatchKMeans(n_clusters=2,
... random_state=0,
... batch_size=6)
>>> kmeans = kmeans.partial_fit(X[0:6,:])
>>> kmeans = kmeans.partial_fit(X[6:12,:])
>>> kmeans.cluster_centers_
array([[2. , 1. ],
[3.5, 4.5]])
>>> kmeans.predict([[0, 0], [4, 4]])
array([0, 1], dtype=int32)
>>> # fit on the whole data
>>> kmeans = MiniBatchKMeans(n_clusters=2,
... random_state=0,
... batch_size=6,
... max_iter=10).fit(X)
>>> kmeans.cluster_centers_
array([[3.95918367, 2.40816327],
[1.12195122, 1.3902439 ]])
>>> kmeans.predict([[0, 0], [4, 4]])
array([1, 0], dtype=int32)
方法
| 方法 | 说明 |
|---|---|
fit(self, X[, y, sample_weight]) |
将其分块成小批, 计算X上的质心, |
fit_predict(self, X[, y, sample_weight]) |
计算聚类中心并预测每个样本的聚类索引 |
fit_transform(self, X[, y, sample_weight]) |
计算聚类并将X变换成簇距离空间 |
get_params(self[, deep]) |
获取此估计器的参数 |
predict(self, X[, sample_weight]) |
预测X中每个样本所属的最接近的聚类 |
score(self, X[, y, sample_weight]) |
K-均值目标上X值的相反 |
set_params(self, **params) |
设置此估计器的参数 |
transform(self, X) |
将X转换为簇距离空间 |
__init__(self, n_clusters=8, *, init='k-means++', max_iter=100, batch_size=100, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init=3, reassignment_ratio=0.01)
初始化self。请参阅help(type(self))以获得准确的说明。
fit(self, X, y=None, sample_weight=None)
通过把它分块成小批,计算X上的质心
| 参数 | 说明 |
|---|---|
| X | array-like or sparse matrix, shape=(n_samples, n_features) 要对训练实例进行聚类。必须注意的是,数据将转换为C顺序,如果给定的数据不是C-连续的,这将导致内存副本 |
| y | Ignored 未使用,在此按约定呈现为API一致性。 |
| sample_weight | array-like, shape (n_samples,), optional X中每个观测值的权重。如果没有,则所有观察值都被赋予相同的权重(默认值:None)。 New in version 0.20. |
| 返回值 | 说明 |
|---|---|
| self | - |
fit_predict(self, X, y=None, sample_weight=None)
计算聚类中心并预测每个样本的聚类索引
方便方法;等价于调用 fit(X)后接predict(X)。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 要转换的新数据 |
| y | Ignored 未使用,在此按约定呈现为API一致性。 |
| sample_weight | array-like of shape (n_samples,), default=None X中每个观测值的权重,如果没有,则所有观测值都被赋予相同的权重。 |
| 返回值 | 说明 |
|---|---|
| labels | ndarray of shape (n_samples,) 每个样本所属的聚类索引 |
fit_transform(self, X, y=None, sample_weight=None)
计算聚类并将X变换成簇距离空间
等效于 fit(X).transform(X),但更有效地实现。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 要转换的新数据 |
| y | Ignored 未使用,在此按约定呈现为API一致性。 |
| sample_weight | array-like of shape (n_samples,), default=None X中每个观测值的权重,如果没有,则所有观测值都被赋予相同的权重。 |
| 返回值 | 说明 |
|---|---|
| labels | array of shape (n_samples, n_clusters) X在新空间中的变换 |
get_params(self, deep=True)
获取此估计器的参数
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为True,则将返回此估计器的参数和所包含的作为估计量的子对象。 |
| 返回值 | 说明 |
|---|---|
| params | mapping of string to any 映射到其值的参数名称 |
partial_fit(self, X, y=None, sample_weight=None)
在单个小型批次X上更新k均值的估计
| 参数 | 说明 |
|---|---|
| X | array-like of shape (n_samples, n_features) 聚类数据点的坐标。必须注意的是,如果X不是C-连续的,它就会被复制。 |
| y | Ignored 未使用,在此按约定呈现为API一致性。 |
| sample_weight | array-like of shape (n_samples,), default=None X中每个观测值的权重,如果没有,则所有观测值都被赋予相同的权重。(默认值:None) |
| 返回值 | 说明 |
|---|---|
| self | - |
predict(self, X, sample_weight=None)
预测X中每个样本所属的最近簇。
在矢量量化文献中,cluster_centers_称为==代码簿==,返回的每个值predict都是代码簿中最接近的代码的索引。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 用于预测的新数据。 |
| sample_weight | array-like, shape (n_samples,), optional X中每个观测值的权重。如果为None,则为所有观测值分配相等的权重(默认值:None)。 |
| 返回值 | 说明 |
|---|---|
| labels | array, shape [n_samples,] 每个样本所属的簇的索引。 |
score(self, X, y=None, sample_weight=None)
K-均值目标上X值的相反
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 新数据 |
| y | Ignored 未使用,在此按约定呈现为API一致性。 |
| sample_weight | array-like of shape (n_samples,), default=None X中每个观测值的权重,如果没有,则所有观测值都被赋予相同的权重。 |
| 返回值 | 说明 |
|---|---|
| score | float 与K-均值目标上的X值相反. |
set_params(self, **params)
设置此估计器的参数
该方法适用于简单估计器以及嵌套对象(例如pipelines)。后者具有表单的 <component>__<parameter>参数,这样就可以更新嵌套对象的每个组件。
| 表格 | 说明 |
|---|---|
| **params | dict 估计器参数 |
| 返回值 | 说明书 |
|---|---|
| self | object 估计器实例 |
transform(self, X)
将X转换为簇距离空间
在新空间中,每个维度都是到聚类中心的距离。注意,即使X是稀疏的,通过transform返回的数组通常也是密集的。
| 参数 | 说明 |
|---|---|
| X | {array-like, sparse matrix} of shape (n_samples, n_features) 新数据 |
| 返回值 | 说明 |
|---|---|
| X_new | ndarray of shape (n_samples, n_clusters) X在新空间中的变换 |