1.7 高斯过程¶

高斯过程Gaussian Processes(GP)是一种通用的有监督学习方法，旨在解决回归和概率分类问题。

高斯过程的优点是：

预测内插了观察结果（至少对于正则核）。
预测结果是概率形式的（高斯形式的）。这样的话，人们可以计算得到经验置信区间并且据此来判断是否需要修改（在线拟合，自适应）在一些区域的预测值。
通用性: 可以指定不同的:核。虽然该函数提供了常用的内核，但是也可以指定自定义内核

高斯过程的缺点包括：

它们不是稀疏的，即它们使用所有样本/特征信息来进行预测。
在高维空间中，当特征数超过几十个时，它们就失去了效率。

1.7.1 高斯过程回归

GaussianProcessRegressor类实现了回归情况下的高斯过程(GP)模型。为此，需要实现指定GP的先验。当参数 normalize_y=False 时，先验的均值通常假定为常数或者零(当 normalize_y=False )，或者训练数据的均值(normalize_y=True)。而先验的方差通过传递 kernel 对象来指定。通过最大化基于传递的 optimizer 的对数边际似然(LML)，内核的超参数可以在高斯过程回归执行拟合过程中被优化。由于 LML 可能会存在多个局部最优解，因此优化过程可以通过指定 n_restarts_optimizer 参数进行多次重复。通过设置内核的超参初始值来进行第一次优化的运行。后续的运行过程中超参值都是从合理范围值中随机选取的。如果需要保持初始化超参值，那么需要把优化器设置为 None。

目标变量中的噪声级别通过参数 alpha 来传递并指定，要么全局是常数要么是一个数据点。请注意，适度的噪声水平也可以有助于处理拟合期间的数字问题，因为它被有效地实现为吉洪诺夫正则化(Tikhonov regularization)，即通过将其添加到核心矩阵的对角线。明确指定噪声水平的替代方法是将 WhiteKernel 组件包含在内核中，这可以从数据中估计全局噪声水平（见下面的示例）。

算法实现是基于 [RW2006]中的算法 2.1 。除了标准 scikit-learn 估计器的 API 之外， GaussianProcessRegressor 的作用还包括：

允许预测，无需事先拟合（基于GP先验）。
提供了一种额外的方法 sample_y(X) , 其评估在给定输入处从 GPR （先验或后验）绘制的样本。
公开了一种方法 log_marginal_likelihood(theta) , 可以在外部使用其他方式选择超参数，例如通过马尔科夫链蒙特卡罗链(Markov chain Monte Carlo)。

1.7.2 GPR示例

1.7.2.1. 带噪声级的 GPR 估计

该示例说明具有包含 WhiteKernel 的和核(sum-kernel)的 GPR 可以估计数据的噪声水平。对数边际似然（LML）的图示表明存在 LML 的两个局部最大值。

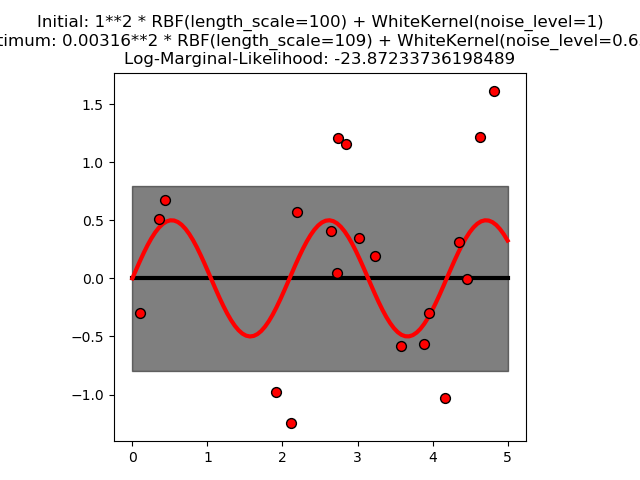第一个模型对应于一个高噪声级和大长度尺度的模型，它解释了噪声对数据的所有变化。

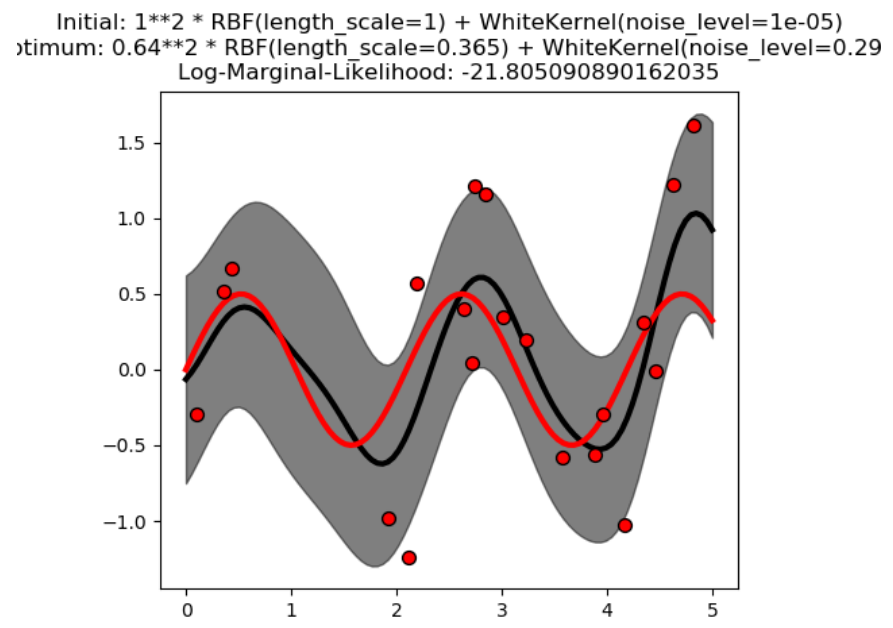第二种方法噪声水平较小，长度尺度较短，主要由无噪声函数关系解释。第二个模型具有较高的可能性，但是，根据超参数的初始值，基于梯度的优化也可能收敛到高噪声的解。因此，对于不同的初始化，多次重复优化是很重要的。

1.7.2.2. GPR 和内核岭回归的比较

内核岭回归(KRR)和GPR都是通过在内部使用“核技巧”来学习目标函数的。KRR在相应核诱导的空间中学习一个线性函数，该函数对应于原始空间中的一个非线性函数。基于带岭正则化的均方误差的损失，选择核空间中的线性函数。GPR利用核函数定义目标函数上先验分布的协方差，并利用观测到的训练数据定义似然函数。基于贝叶斯定理（Bayes theorem），定义了目标函数上的(高斯)后验分布，其均值用于预测。

一个主要的区别是，GPR可以基于边缘似然函数的梯度上升来选择核的超参数，而KRR需要对交叉验证的损失函数(均方误差损失)执行网格搜索。另一个不同之处在于，GPR学习目标函数的生成概率模型，因此可以提供有意义的置信区间和后验样本以及预测，而KRR只提供预测。

下图说明了人工数据集上的两种方法，该数据集由一个正弦目标函数和强噪声组成。该图比较了KRR模型和基于ExpSineSquared核的GPR的模型，ExpSineSquared核适用于学习周期函数。核的超参数控制核的光滑性(长尺度)和周期性(周期性)。此外，数据的噪声水平是由GPR通过内核中附加的WhiteKernel成分和KRR的正则化参数α显式地获得的。

该图显示，这两种方法都学习了目标函数的合理模型。GPR正确地识别出函数的周期约为2∗π(6.28)，而KRR选择的周期为2倍周期4∗π。基于此，GPR为KRR的预测提供了合理的置信边界。这两种方法的一个主要区别是拟合和预测所需的时间：原则上，虽然拟合KRR在是快速的，但网格搜索的超参数优化规模与超参数的数量成指数关系(“维数诅咒”)。基于梯度优化的GPR参数不受这种指数标度的影响，因此在这个具有三维超参数空间的例子中，速度要快得多。预测的时间是相似的，然而，GPR产生预测分布的方差要比仅仅预测平均值花费的时间要长得多。

1.7.2.3 Mauna Loa CO2 数据上的 GPR

此示例基于[RW2006]第5.4.3节。给出了一个基于对数边际似然梯度上升的复杂核工程和超参数优化的实例。这些数据包括1958年至1997年期间在夏威夷莫纳洛阿观测站收集的大气二氧化碳平均浓度(按体积计算，以百万分之数(Ppmv)计)。目的是模拟二氧化碳浓度随时间t的变化。

核由几个术语组成，它们负责解释信号的不同属性：

一个长期的，平稳的上升趋势可以用RBF核来解释。长尺度较大的径向基函数(RBF)内核强制成平滑，没有强制趋势上升，这就留给GP选择。长度、比例尺和振幅是自由的超参数。
季节性因素，由定期的 ExpSineSquared 内核解释，固定周期为1年。该周期分量的长度尺度控制其平滑度是一个自由参数。为了使准确周期性的衰减，采用带有RBF内核的产品。该RBF组件的长度尺寸控制衰减时间，并且是另一个自由参数。
较小的中期不规则性将由 RationalQuadratic 核来解释， RationalQuadratic 内核组件的长度尺度和 alpha 参数决定长度尺度的扩散性。根据[RW2006]，这些不规则性可以更好地由 RationalQuadratic 来解释，而不是 RBF 核，这可能是因为它可以容纳几个长度尺度。
“noise(噪声)” 一词，由一个 RBF 内核贡献组成，它将解释相关的噪声分量，如局部天气现象以及 WhiteKernel 对白噪声的贡献。相对幅度和RBF的长度尺度是进一步的自由参数。

在减去目标平均值后最大化对数边际似然产生下列内核，其中LML为-83.214:

34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
                                                   periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)

因此，大多数目标信号（34.4ppm）由长期上升趋势（长度为41.8年）解释。周期分量的振幅为3.27ppm，衰减时间为180年，长度为1.44。长时间的衰变时间表明我们在当地非常接近周期性的季节性成分。相关噪声的幅度为0.197ppm，长度为0.138年，白噪声贡献为0.197ppm。因此，整体噪声水平非常小，表明该模型可以很好地解释数据。该图还显示，该模型直到2015年左右才能做出置信度比较高的预测

1.7.3 高斯过程分类(GPC)

GaussianProcessClassifier 将高斯过程(GP)用于分类，更具体地说，用于概率分类，其中测试预测采用类概率的形式。高斯过程分类器将GP放在一个隐函数上，然后通过一个链接函数来获得概率分类。隐函数是一种所谓的干扰函数( nuisance function)，它的值是不被观察到的，并且它们本身并不相关。其目的是为了方便地制定模型，并在预测过程中删除(整合)。GaussianProcessClassfier实现了逻辑链函数，它不能解析地计算积分，但在二进制情况下很容易逼近。

与回归设置相反，即使设置了高斯过程先验，隐函数的后验也不符合高斯分布，因为高斯似然不适用于离散类标签。相反，使用的是与逻辑链接函数对应的非高斯似然。 GaussianProcessClassifier 通过拉普拉斯近似(Laplace approximation)来估计非高斯后验分布。更多详细信息，请参见[RW2006]的第 3 章。

GP先验平均值假定为零。先验的协方差是通过传递kernel对象来指定的。在通过最大化基于传递的对数边际似然（LML）的 GaussianProcessRegressor 拟合期间，优化内核的超参数 optimizer 。由于LML可能具有多个局部最优值，所以优化器可以通过指定 n_restarts_optimizer 进行重复。第一次运行始终从内核的初始超参数值开始执行; 从已经从允许值的范围中随机选择超参数值来进行后续运行。如果初始超参数需要保持固定，None可以传递给优化器。

GaussianProcessClassifier 通过执行基于OvR(one-versus-rest)或 OvO(one-versus-one )策略的训练和预测来支持多类分类。在OvR(one-versus-rest)策略中，每个类都配有一个二分类高斯过程分类器，该类别被训练为将该类与其余类分开。在 “one_vs_one” 中，对于每对类拟合一个二进制高斯过程分类器，这被训练为分离这两个类。这些二分类的预测的预测被组合成多类预测。更多详细信息，请参阅multi-class classification 。

在高斯过程分类的情况下，”one_vs_one” 策略可能在计算上更廉价，因为它只决涉及整个训练集的一个子集的许多问题，而不是整个数据集的较少的问题。由于高斯过程分类与数据集的大小相互立方，这可能要快得多。但是，请注意，”one_vs_one” 不支持预测概率估计，而只是简单的预测。此外，请注意， GaussianProcessClassifier 在内部还没有实现真正的多类拉普拉斯逼近，但如上所述，在解决内部二分类任务的，基于的是使用one-versus-rest 或者 one-versus-one方法。

1.7.4 GPC实例

1.7.4.1 GPC概率预测

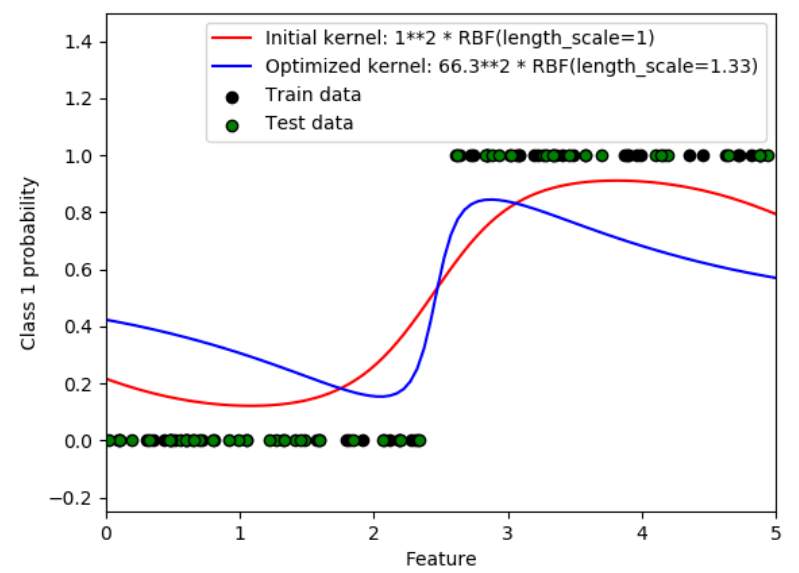
这个例子说明了在不同的超参数选择下，RBF核的GPC的预测概率。第一个图显示了具有任意选择的超参数和对应于最大对数边际似然(LML)的超参数的GPC的预测概率。

虽然通过优化LML选择的超参数具有相当大的LML，但根据测试数据的日志丢失情况，它们的性能稍差。图中显示，这是因为它们在类边界上出现了类概率的急剧变化(这是好的)，但是预测的概率接近于离类边界近0.5(这是不好的)，这种不良影响是由GPC内部使用的拉普拉斯逼近引起的。

第二个图显示了内核的超参数的不同选择的日志边缘可能性，突出显示了在第一个图形中使用黑点的两个超参数选择。

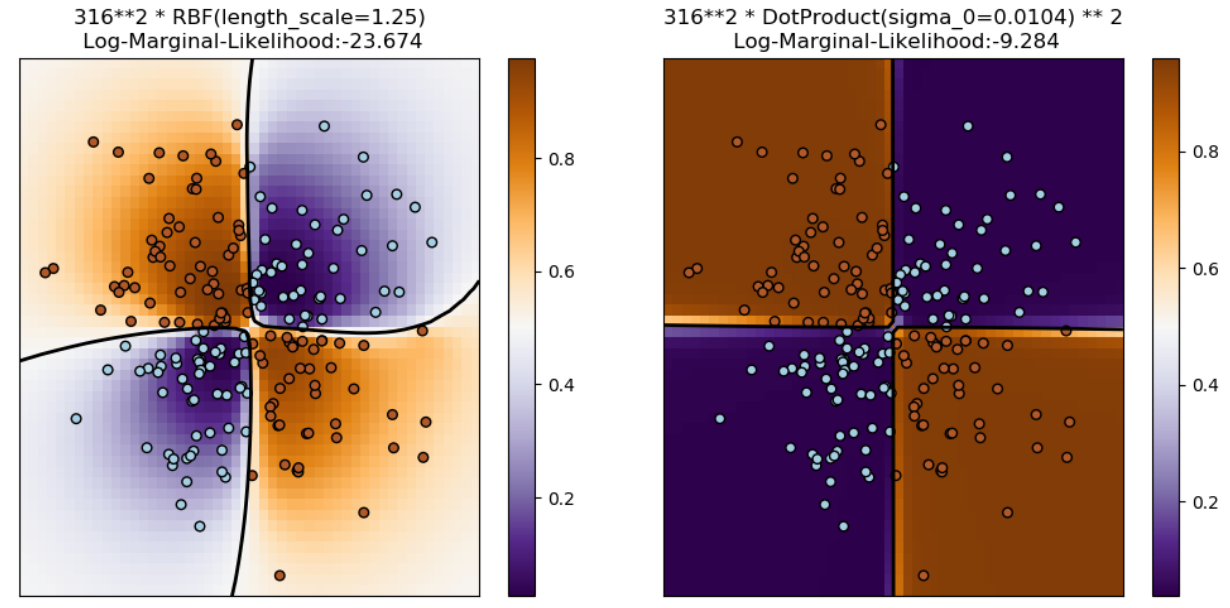
1.7.4.2 XOR数据集上GPC的说明

此示例说明XOR数据上的GPC。比较了固定、各向同性核(RBF)和非固定核(DotProduct)。在这个特定的数据集上，DotProduct内核获得了更好的结果，因为类边界是线性的，并且与坐标轴重合。然而，在实践中，像 RBF这样的固定内核往往获得更好的结果。

1.7.4.3 iris数据集上的高斯过程分类

该示例说明了用于iris数据集的二维版本上各向同性和各向异性RBF核的GPC的预测概率。这说明了GPC对多类分类的适用性。各向异性RBF内核通过为两个特征维度分配不同的长度尺度来获得稍高的LML（对数边际似然）。

1.7.5 高斯过程内核

核(也称GPs中的协方差函数)是GPs的一个重要组成部分，它决定GP的先验和后验形状。它们通过定义两个数据点的“相似性”，并结合相似的数据点应该具有相似的目标值的假设，对正在学习的函数进行编码。内核可以分为两类：固定内核，只取决于两个数据点的距离，不依赖于它们的绝对值 , 因此它们对于输入空间中的转换是不变的；非固定的内核，取决于数据点的具体值。固定内核可以进一步细分为各向同性和各向异性内核，其中各向同性内核不会在输入空间中旋转。有关更多细节，我们参考[RW2006]第4章。关于如何最佳组合不同内核，我们可以参考[Duv2014]。

1.7.5.1 高斯过程核API

内核 Kernel 的主要用途是计算数据点之间的GP协方差。为此，可以调用内核的方法__call___。该方法既可用于计算二维数组X中所有成对数据点的“自协方差”，也可用于计算二维数组X与二维数组Y中的成对数据点的所有组合的“交叉协方差”。以下恒等式适用于所有内核k( WhiteKernel除外)：k(X) == K(X, Y=X)

如果只使用自协方差的对角线，则可以调用内核的diag()方法，这比对___call__: np.diag(k(X, X)) == k.diag(X)的等效调用计算效率更高。

核由超参数的向量参数化。例如，这些超参数可以控制内核的长度、尺度或周期(见下文)。所有内核都支持计算内核相对于的自协方差的分析梯度，方法是在__call__方法中设置eval_gradient=True。这一梯度被高斯过程(包括回归者和分类器)用于计算对数边际似然的梯度，而后者又被用来确定的值，该值通过梯度上升来最大化对数边际似然。对于每个超参数，在创建内核实例时需要指定初始值和边界。可以通过内核对象的属性theta获取和设置的当前值。此外，可以通过内核的bounds属性来访问超参数的边界。请注意，这两个属性(theta 和 bounds)都返回内部使用的值的对数转换值，因为这些值通常更适合基于梯度的优化。每个超参数的规范以Hyperparameter实例的形式存储在各自的内核中。请注意，使用名称为“x”的超参数的内核必须具有属性sel.x和self.x_bounds。

所有内核的抽象基类都是 Kernel。内核实现了与Estimator类似的接口，提供了get_params()、set_params()和clone()方法。这还允许通过元估值器(如Pipeline or GridSearch)设置内核值。注意，由于内核的嵌套结构(通过应用内核运算符，请参见下面)，内核参数的名称可能变得相对复杂。通常，对于二进制核运算符，左操作数的参数以K1__为前缀，右操作数的参数以K2_为前缀。另一种方便的方法是clone_with_theta(theta)，它返回内核的克隆版本，但超参数设置为theta。一个例子进行说明：

>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta)  # Note: log-transformed
[ 0.         -0.69314718  0.69314718]
>>> print(kernel.bounds)  # Note: log-transformed
[[      -inf 2.30258509]
 [      -inf 2.30258509]
 [      -inf 2.30258509]]

所有的高斯过程核都可以与sklearn.metrics.pairwise互操作，反之亦然：内核的子类的实例可以作为metric传递给 sklearn.metrics.pairwise中的pairwise_kernels。此外，可以通过使用包装器类 PairwiseKernel，可以将来自的pairwise内核函数用作GP内核。唯一的警告是，超参数的梯度不是解析的，而是数值的，所有这些核都只支持各向同性距离。参数gamma被认为是一个超参数，可以被优化。其他内核参数在初始化时直接设置，并保持固定。

1.7.5.2 基础核

ConstantKernel内核可以用作 Product内核的一部分，它可以缩放其他因素(内核)的大小，也可以作为Sum内核的一部分，其中它调整了高斯过程的平均值。它取决于参数 constant_value。它的定义是：

WhiteKernel内核的主要用例是 sum-kernel 的一部分，它解释了信号的噪声部分。调整其参数noise_level对应于估计其噪声水平。它的定义是：

1.7.5.3 核操作

内核运算符获取一个或两个基本内核，并将它们组合成一个新的内核。 Sum核取两个核和，并通过组合它们。Product内核采用两个内核和，并通过组合它们。Exponentiation核取一个基本核和一个标量参数，通过组合它们，注意在核对象上重写了魔术方法___add__, __mul___ 和 __pow__ ，因此可以使用例如RBF() + RBF()作为 Sum(RBF(), RBF())的快捷方式。

1.7.5.4 径向基函数(RBF)核

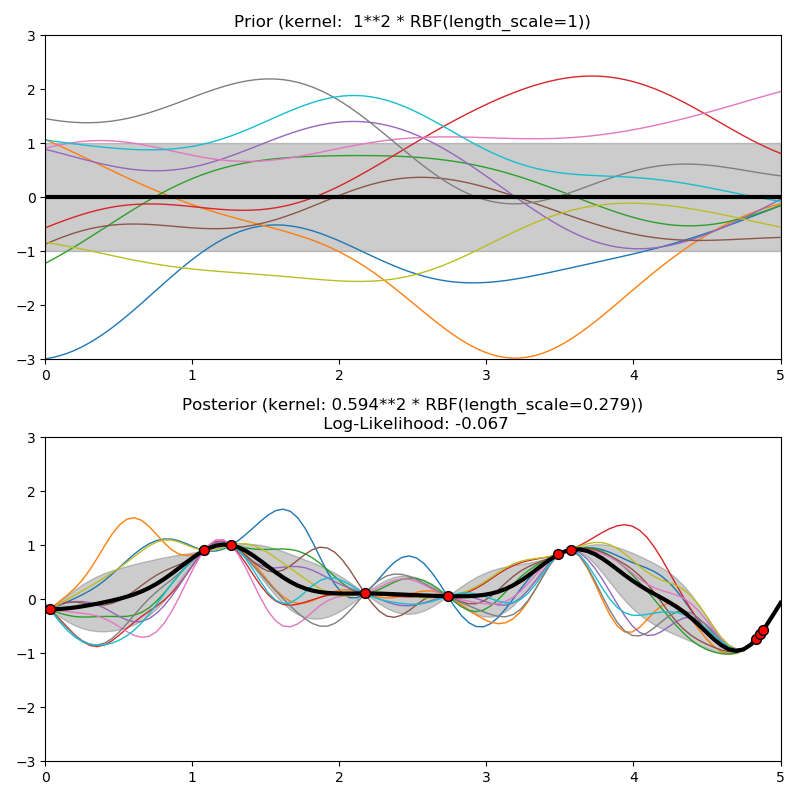
RBF核是一个稳定的核函数。它也被称为“平方指数”核。它由一个长度尺度参数参数来参数化，它既可以是一个标量(核的各向同性变体)，也可以是一个与输入x(核的各向异性变量)相同维数的向量。内核由以下几个方面提供：

其中是欧氏距离。这个核是无穷可微的，这意味着以这个核作为协方差函数的GPs具有所有阶的均方导数，因此是非常光滑的。由RBF核产生的GP的先验和后验如下图所示：

1.7.5.5 Matérn核

Matern核是一个平稳核，是RBF核的推广。它有一个额外的参数，它控制结果函数的光滑性。它由一个长度尺度参数参数来参数化，它既可以是一个标量(核的各向同性变体)，也可以是一个与输入x(核的各向异性变量)相同维数的向量。该核由以下几个方面提供：

其中是欧氏距离，是修正的 Bessel 函数，是伽马函数。随着，Matérn核收敛于径向基函数核（RBF）。当时，Matérn核与绝对指数核(absolute exponential kernel)相同，即，

特别地， :

并且，:

学习函数的流行选择不是无限可微(由径向基函数核(RBF)假设)，而是至少一次()或两次可微()。

通过控制学习函数的光滑性的灵活性允许适应真正的底层函数关系的性质。由Matérn核产生的GP的先验和后验如下图所示：

有关Matérn内核的不同变体的更多详细信息，请参见 [RW2006]，pp 84。

1.7.5.6 有理二次核

RationalQuadratic（有理二次核）可以看作是具有不同特征长度尺度的 RBF核的尺度混合(无限和)。它由长度尺度参数和尺度混合参数来参数化，此时只支持各向同性变量，其中是标量。该核由下式给出：

由 RationalQuadratic产生的GP的先验和后验如下图所示：

1.7.5.7 Exp-Sine-Squared核

ExpSineSquared内核允许对周期性函数进行建模。它由长度尺度参数和周期参数来参数化.现在只有各向同性变量，其中是标量。该核由以下几个方面提供：

由ExpSineSquared内核产生的GP的先验和后验如下图所示：

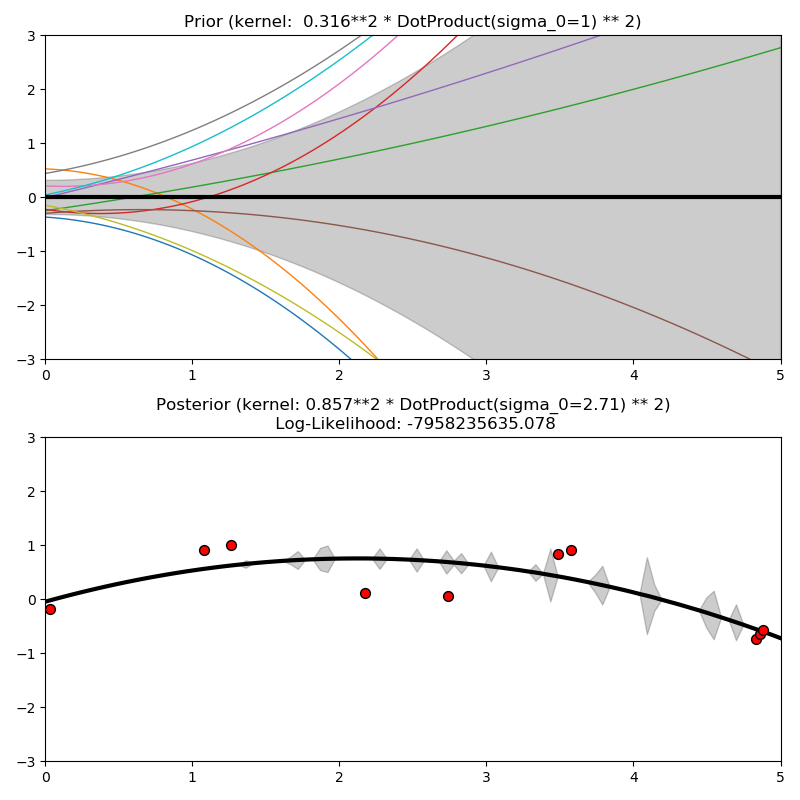
1.7.5.8 点积核

DotProduct核是非平稳的，可以通过在线性回归的系数上加上的先验和在偏置上加上的先验得到。 DotProduct核不受原点坐标旋转的影响，但不是转换。它由参数参数化。对于，内核被称为齐次线性核，否则它是非齐次的。内核由下式给出：

DotProduct 核通常与指数结合在一起。指数为2的示例如下图所示：

1.7.5.9 参考文献

RW2006(1,2,3,4,5,6) Carl Eduard Rasmussen and Christopher K.I. Williams, “Gaussian Processes for Machine Learning”, MIT Press 2006, Link to an official complete PDF version of the book here .

Duv2014 David Duvenaud, “The Kernel Cookbook: Advice on Covariance functions”, 2014, Link .