sklearn.gaussian_process.DotProduct¶
class sklearn.gaussian_process.kernels.DotProduct(sigma_0=1.0, sigma_0_bounds=(1e-05, 100000.0))
点积核是非平稳的,可以通过对的系数加先验通过线性回归得到 和一个先验上的偏置。点积核对于坐标绕原点的旋转是不变的,但不是平动的。它由控制内核不均匀性的参数sigma_0参数参数化。为核称为齐次线性核,否则是非齐次的。核函数是
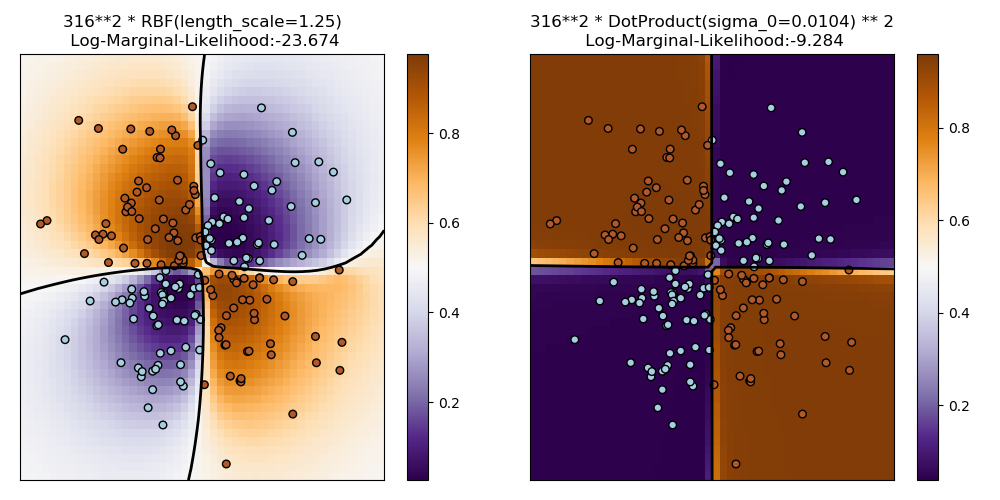
DotProduct内核通常与求幂结合使用。
请参阅,第4章4.2节,以获得关于DotProduct内核的更多细节。
在用户指南中阅读更多内容。
新版本0.18。
| 参数 | 说明 |
|---|---|
| sigma_0 | float >= 0, default=1.0 控制核不均匀性的参数。如果sigma_0=0,则内核是同质的。 |
| sigma_0_bounds | pair of floats >= 0 or “fixed”, default=(1e-5, 1e5) sigma_0的上下限。如果设置为“fixed”,则在超参数调优期间无法更改“sigma_0”。 |
| 属性 | 说明 |
|---|---|
bounds |
返回的对数变换界限。 |
| hyperparameter_constant_value | |
hyperparameters |
返回所有超参数规范的列表。 |
n_dims |
返回内核的非固定超参数的数量。 |
requires_vector_input |
返回内核是否定义在离散结构上。 |
theta |
返回(扁平的、对数转换的)非固定超参数。 |
示例
>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel
>>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
>>> kernel = DotProduct() + WhiteKernel()
>>> gpr = GaussianProcessRegressor(kernel=kernel,
... random_state=0).fit(X, y)
>>> gpr.score(X, y)
0.3680...
>>> gpr.predict(X[:2,:], return_std=True)
(array([653.0..., 592.1...]), array([316.6..., 316.6...]))
方法
| 方法 | 说明 |
|---|---|
__call__(self, X[, Y, eval_gradient]) |
返回核函数k(X, Y)和它的梯度。 |
clone_with_theta(self, theta) |
返回带有给定超参数theta的self的克隆。 |
diag(self, X) |
返回核函数k(X, X)的对角线。 |
get_params(self[, deep]) |
获取这个内核的参数。 |
is_stationary(self) |
返回内核是否静止。 |
set_params(self, **params) |
设置这个内核的参数。 |
__init__(self, sigma_0=1.0, sigma_0_bounds=(1e-05, 100000.0))
初始化self. See 请参阅help(type(self))以获得准确的说明 。
__call__(self, X, Y=None, eval_gradient=False)
返回核函数k(X, Y)和它的梯度。
| 参数 | 说明 |
|---|---|
| X | ndarray of shape (n_samples_X, n_features) 返回核函数k(X, Y)的左参数 |
| Y | ndarray of shape (n_samples_Y, n_features), default=None 返回的核函数k(X, Y)的正确参数。如果没有,则计算k(X, X)。 |
| eval_gradient | bool, default=False 确定关于核超参数的梯度是否确定。只有当Y没有的时候才被支持。 |
| 返回值 | 说明 |
|---|---|
| K | ndarray of shape (n_samples_X, n_samples_Y) 内核k (X, Y) |
| K_gradient | ndarray of shape (n_samples_X, n_samples_X, n_dims), optional 核函数k(X, X)关于核函数超参数的梯度。只有当eval_gradient为真时才返回。 |
property bounds
返回的对数变换界限。
| 返回值 | 说明 |
|---|---|
| bounds | ndarray of shape (n_dims, 2) 核函数超参数的对数变换界限 |
clone_with_theta(self, theta)
返回带有给定超参数theta的self的克隆。
| 返回值 | 说明 |
|---|---|
| theta | ndarray of shape (n_dims,) 的hyperparameters |
diag(self, X)
返回核函数k(X, X)的对角线。
该方法的结果与np.diag(self(X))相同;但是,由于只计算对角,因此可以更有效地计算它。
| 参数 | 说明 |
|---|---|
| X | ndarray of shape (n_samples_X, n_features) 返回的核函数k(X, Y)的左参数。 |
| 返回值 | 说明 |
|---|---|
| K_diag | ndarray of shape (n_samples_X,) 核k(X, X)的对角线 |
get_params(self, deep=True)
获取这个内核的参数。
| 参数 | 说明 |
|---|---|
| deep | bool, default=True 如果为真,将返回此估计器的参数以及包含的作为估计器的子对象。 |
| 返回值 | 说明 |
|---|---|
| params | dict 参数名称映射到它们的值。 |
property hyperparameters
返回所有超参数规范的列表。
is_stationary(self)
返回内核是否静止。
property n_dims
返回内核的非固定超参数的数量。
property requires_vector_input
返回内核是在固定长度的特征向量上定义的还是在通用对象上定义的。向后兼容性的默认值为True。
set_params(self, **params)
设置这个内核的参数。
该方法适用于简单估计量和嵌套对象(如pipline)。后者具有形式为<component>_<parameter>的参数,这样就让更新嵌套对象的每个组件成为了可能。
设置这个内核的参数。
| 返回值 | 说明 |
|---|---|
| self | 无 |
property theta
返回(扁平的、对数转换的)非固定超参数。
注意,theta通常是内核超参数的对数变换值,因为这种搜索空间的表示更适合超参数搜索,因为像长度尺度这样的超参数自然存在于对数尺度上。
| 返回值 | 说明 |
|---|---|
| theta | ndarray of shape (n_dims,) 核函数的非固定、对数变换超参数 |