1.2 线性和二次判别分析¶
线性判别分析(discriminant_analysis.LinearDiscriminantAnalysis) 和二次判别分析(discriminant_analysis.QuadraticDiscriminantAnalysis) 是两种经典的分类器,如它们的名字所示,分别具有线性和二次决策平面。
这些分类器之所以有吸引力,是因为它们有一些的解析解,可以很容易地计算出,本质上是多分类的,在实践中证明工作良好,并且没有需要调优的超参数。
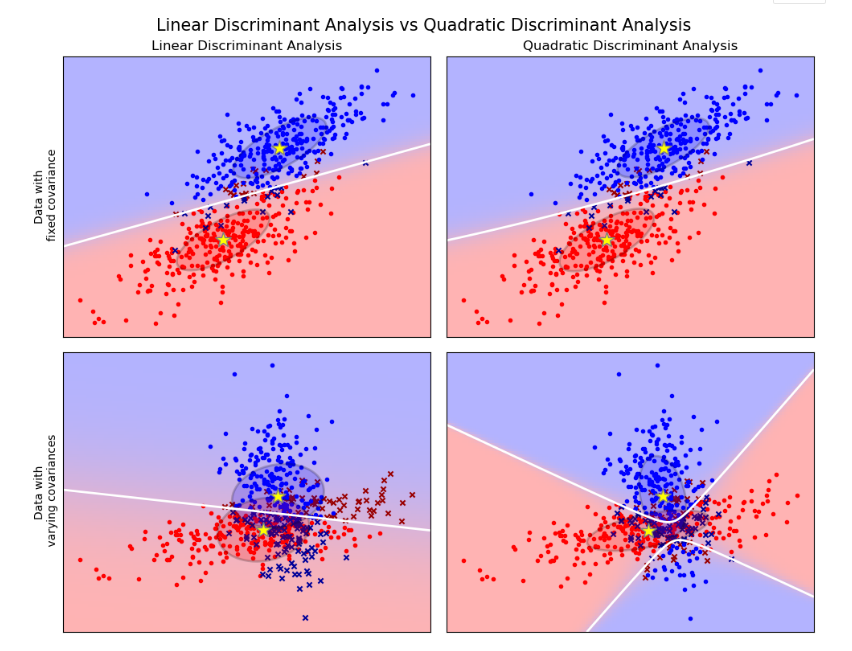
图中给出了线性判别分析和二次判别分析的决策边界。底部那行证明线性判别分析只能学习线性边界,而二次判别分析可以学习二次边界,因此具有更大的灵活性。
| 示例 |
|---|
| 协方差椭球的线性和二次判别分析LDA和QDA在人造数据上的比较 |
1.2.1.基于线性判别分析的降维方法
discriminant_analysis.LinearDiscriminantAnalysis 可用于执行有监督的降维,方法是将输入数据投影到一个线性子空间,该空间由使类与类之间的分离最大化的方向组成(在下面的数学部分中讨论的准确意义)。输出的维数必然小于类的数量,因此,一般来说,这是一个相当强的降维,并且只有在多类设置中才有意义。
算法的实现是在discriminant_analysis.LinearDiscriminantAnalysis.transform, 可以使用 n_components参数设置所需的维数。这个参数对discriminant_analysis.LinearDiscriminantAnalysis.fit或者 discriminant_analysis.LinearDiscriminantAnalysis.predict没有影响。
| 示例 |
|---|
| 在lris数据集上比较LDA和PCA:基于lris数据集比较LDA和PCA的降维方法 |
1.2.2 LDA和QDA分类器的数学表达式
LDA和QDA都可以从简单的概率模型中推导出来,这种概率模型模拟了每一类中的数据的条件分布,然后,就可以利用贝叶斯公式进行预测:
我们选择可以使得上述条件概率最大化的。
更具体地说,对于线性和二次判别分析,被建模为具有密度的多元高斯分布:
其中是特征的数目。
1.2.2.1 QDA
根据上面的模型,后验的对数为:
常数项对应于分母 ,以及其他来自高斯的常数项。预测类是使这种对数后验最大化的类。
| 注意:与高斯朴素贝叶斯的关系 |
|---|
如果在QDA模型中,假设协方差矩阵是对角矩阵,在每个类中,输入都是条件独立的,那么所得到的分类器等价于高斯朴素贝叶斯分类器naive_bayes.GaussianNB。 |
1.2.2.2 LDA
LDA是QDA的特例,其中假设每个类别的高斯都共享相同的协方差矩阵: (对所有)。这将对数后验减少到:
对应在样本 与均值样品之间的马氏距离(Mahalanobis Distance)。马氏距离表示距离均值的远近程度,同时还要考虑每个特征的方差。因此,我们可以将LDA解释为根据马氏距离把分配给最接近平均值的类,同时也考虑了类的先验概率。
LDA的对数后验也可以写为[3]:
and 。这些数量分别对应于coef_和intercept_属性。
由上式可知,LDA具有一个线性决策曲面。对于QDA,没有对协方差矩阵的高斯的假设 ,导致二次决策曲面。详见 [1] 。
1.2.3 LDA降维的数学公式
首先请注意,表示 是 中的向量,并且导致 产生至少 个仿射子空间(2点在一条线上,3点在一条平面上,依此类推)。
如上所述,我们可以将LDA解释为分配 x 对那些卑鄙的人 μk在最接近马氏距离上最接近,同时也考虑了该类的先验概率。或者,LDA等效于首先对数据进行球化处理,以使协方差矩阵为单位,然后分配x 以欧几里得距离最接近均值(仍占先验类)。
如上所述,我们可以将LDA解释为分配 给其在马氏距离中是最接近均值的类,同时也考虑了类的先验概率。或者,LDA等价于首先将数据球化,以协方差矩阵作为单位,然后根据欧氏距离分配最接近的平均值(仍然考虑类先验)。
计算此 维空间中的欧几里得距离等同于首先将数据点投影到 维空间中,然后计算距离(因为其他维度在距离方面将对每个类别均等地做出贡献)。换句话说,如果 在原始空间中最接近 ,情况也会如此 。这说明,在LDA分类器中,通过线性投影到 K−1 维空间。
通过投影到线性子空间上, 使得投影后的的方差最大化, (事实上, 我们是对类的均值)做了主成分分析(PCA), 我们就能进一步的降维, 知道达到。这个L对应于transform方法中使用的参数 n_components 。有关更多详细信息,请参见 [1]。
1.2.4 收缩(Shrinkage)
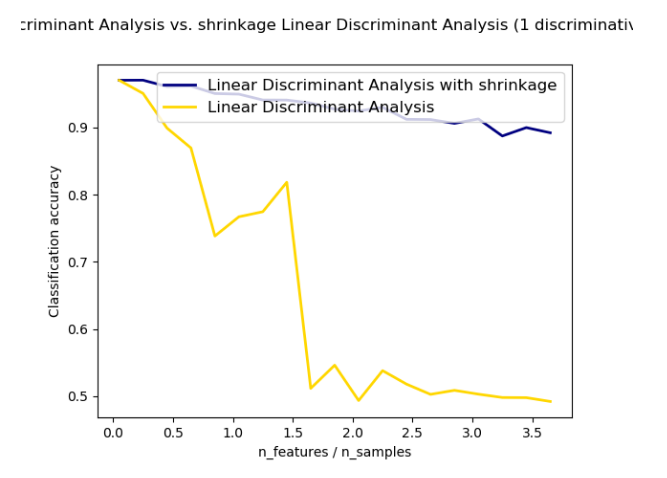
收缩(Shrinkage)是在训练样本数相对于特征数较少的情况下改进协方差矩阵估计的一种工具。在这种情况下,经验样本协方差是一个很差的预测器。Shrinkage LDA可以通过在 discriminant_analysis.LinearDiscriminantAnalysis中将参数shrinkage设置为‘auto’来使用。这里自动确定最优的Shrinkage的参数的方法主要是依据Ledoit and Wolf [4]中所提到的理论。注意, Shrinkage要想起作用, 只有将参数 solver设置为 ‘lsqr’ or ‘eigen’。
shrinkage参数也可以手动设置在0到1之间。特别地是,0对应于没有收缩(这意味着将使用经验协方差矩阵),而1对应于完全收缩(这意味着方差的对角矩阵将用作协方差矩阵的估计)。将此参数设置为这两个极值之间的值将估计一个协方差矩阵的收缩版本。
1.2.5 预估算法
使用LDA和QDA需要计算后验对数,这取决于类的先验 ,该类表示以及协方差矩阵。
“ svd”求解器是用默认求解器 LinearDiscriminantAnalysis,并且是 QuadraticDiscriminantAnalysis唯一可用的求解器。它可以执行分类和转换(对于LDA)。由于它不依赖于协方差矩阵的计算,“svd”求解器在特征数量较大的情况下可能更可取。'svd'求解器不能与收缩一起使用。SVD求解器的使用依赖于协方差矩阵 ,根据定义,等于 ,来自(居中)矩阵的SVD:。事实证明,我们可以计算 上面的对数后验,而不必显式计算:通过的SVD足够计算 S 和 V 。对于LDA,将计算两个 SVD:居中输入矩阵的SVDX以及类均值向量的SVD。
“ lsqr”求解器是仅适用于分类的高效算法。它需要显式计算协方差矩阵,并支持收缩。该求解器计算系数通过解决 ,从而避免了对逆的显式计算。
‘eigen’ 解决器是基于类散度与类内离散率之间的优化。 它可以被用于分类以及转换,此外它还同时支持收缩。然而该解决方案需要计算协方差矩阵,因此它可能不适用于具有大量特征的情况。
| 示例 |
|---|
| 正态和收缩线性判别分析在分类中的应用:带收缩和不收缩LDA分类器的比较 |
参考资料:
1(1,2)“The Elements of Statistical Learning”, Hastie T., Tibshirani R., Friedman J., Section 4.3, p.106-119, 2008. 2Ledoit O, Wolf M. Honey, I Shrunk the Sample Covariance Matrix. The Journal of Portfolio Management 30(4), 110-119, 2004. 3R. O. Duda, P. E. Hart, D. G. Stork. Pattern Classification (Second Edition), section 2.6.2.




