6.6 随机投影

sklearn.random_projection模块实现了一种简单且计算高效的减少数据维数的方式，通过以可控制的精度（以附加方差）为代价来缩短处理时间并缩小模型尺寸。该模块实现两种非结构化随机矩阵： 高斯随机矩阵和 稀疏随机矩阵。

控制随机投影矩阵的尺寸和分布以维持数据集的任何两个样本之间的成对距离。因此，随机投影是基于距离方法的合适的近似技术。

参考文献：

  • Sanjoy Dasgupta.2000. 随机投影实验。 第16届人工智能不确定性会议（UAI'00）的会议记录，克雷格·鲍迪埃（Craig Boutilier）和MoisésGoldszmidt（编辑）。美国加利福尼亚州旧金山的摩根考夫曼出版社（Morgan Kaufmann Publishers Inc.），编号143-151。
  • Ella Bingham和Heikki Mannila.2001. 降维中的随机投影：图像和文本数据的应用。 第七届ACM SIGKDD有关知识发现和数据挖掘的国际会议论文集（KDD '01）。美国纽约州纽约市，ACM，245-250。

6.6.1 The Johnson-Lindenstrauss 引理

随机投影效率背后的主要理论结果是 Johnson-Lindenstrauss引理（引用Wikipedia）：

在数学中，Johnson-Lindenstrauss引理是关于点从高维到低维欧几里德空间的低失真嵌入的结果。引理指出，高维空间中的一小部分点可以以点之间的距离几乎被保留的方式嵌入到低维空间中。用于嵌入的地图至少为Lipschitz，甚至可以视为正交投影。

仅知道样本数的情况下， sklearn.random_projection.johnson_lindenstrauss_min_dim保守估计随机子空间的最小尺寸，以保证随机投影导致的失真在一定范围内：

>>> from sklearn.random_projection import johnson_lindenstrauss_min_dim
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=0.5)
663
>>> johnson_lindenstrauss_min_dim(n_samples=1e6, eps=[0.5, 0.1, 0.01])
array([    663,   11841, 1112658])
>>> johnson_lindenstrauss_min_dim(n_samples=[1e4, 1e5, 1e6], eps=0.1)
array([ 7894,  9868, 11841])

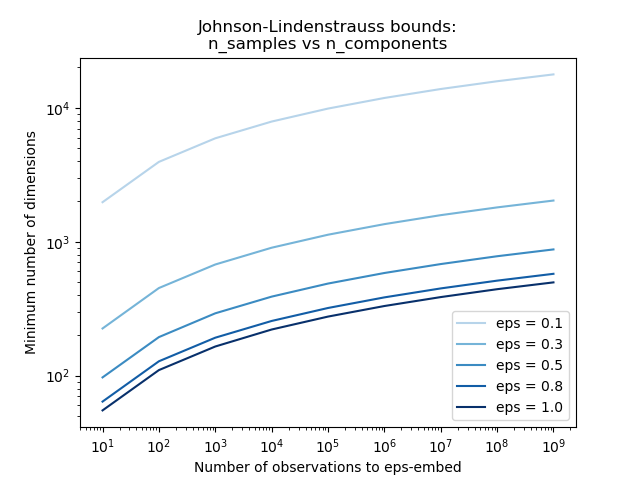
示例：

参考文献：

6.6.2 高斯随机投影

sklearn.random_projection.GaussianRandomProjection通过将原始输入控件投影到随机生成的矩阵上来降低维数，该矩阵从以下分布 中提取元素。

以下片段说明了如何使用高斯随机投影转换器：

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.GaussianRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

6.6.3 稀疏随机投影

sklearn.random_projection.SparseRandomProjection通过使用稀疏随机矩阵投影原始输入空间来降低维数。

稀疏随机矩阵是稠密高斯随机投影矩阵的替代并保证相似的嵌入质量，同时具有更高的存储效率而且可以更快地计算投影数据。

如果我们定义s = 1 / density，则随机矩阵的元素来自：

其中是投影子空间的大小。 默认情况下，非零元素的密度设置为Ping Li等人建议的最小密度：.

以下小片段说明了如何使用稀疏随机投影转换器：

>>> import numpy as np
>>> from sklearn import random_projection
>>> X = np.random.rand(100, 10000)
>>> transformer = random_projection.SparseRandomProjection()
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)

参考文献