2.1. 高斯混合模型¶
sklearn.mixture是一种采用高斯混合模型进行非监督学习的包,(支持 diagonal,spherical,tied,full 四种类型的协方差矩阵)可以对数据进行采样并估计,同时该包也提供了帮助用户决定合适分量个数的功能。
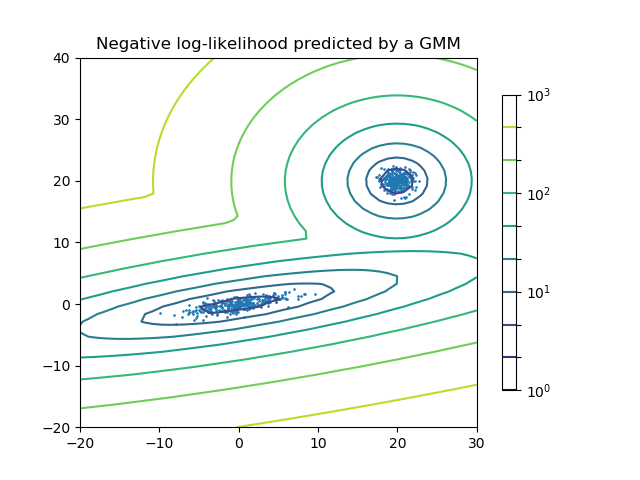 二分量高斯混合模型: 数据点,以及模型的等概率线。
二分量高斯混合模型: 数据点,以及模型的等概率线。
高斯混合模型是一种概率模型,它假设所有数据点都是从有限数量的高斯分布的混合参数中生成的。可以将混合模型视为对 k-means聚类算法的扩展,它包含了数据的协方差结构以及隐高斯模型中心的信息。
对于不同的估算策略,Scikit-learn采用不同的类来预测高斯混合模型。下面将详细介绍:
2.1.1. 高斯混合
该GaussianMixture对象实现了用于拟合高斯混合模型的 期望最大化(EM)算法。它还可以为多元模型绘制置信椭圆体,并计算贝叶斯信息准则以评估数据中的聚类数量。GaussianMixture.fit可以从训练数据中拟合出一个高斯混合模型。在给定测试数据的情况下,使用该GaussianMixture.predict方法可以为每个样本分配最适合它的高斯分布模型。。
GaussianMixture带有不同的选项来约束不同的的协方差估计:spherical,diagonal,tied 或 full 协方差。

示例:
一个利用高斯混合模型在鸢尾花卉数据集(IRIS 数据集)上做聚类的协方差实例,请查阅 GMM协方差 一个绘制密度估计的示例,请查阅 高斯混合模型的密度估计
2.1.1.1. 优缺点GaussianMixture
2.1.1.1.1 优点
速度:它是混合模型学习算法中的最快算法 无偏差性:由于此算法仅最大化可能性,因此不会使均值趋于零,也不会使聚类大小具有可能适用或不适用的特定结构。
2.1.1.1.2 缺点
奇异性:当每个混合模型的点数不足时,估计协方差矩阵将变得困难,并且除非对协方差进行人为正则化,否则该算法会发散并寻找无穷大似然函数值的解。 分量数量:该算法将始终使用它可以使用的所有分量,所以在没有外部提示的情况下,需要留存数据或者信息理论标准来决定用多少个分量。
2.1.1.2. 选择经典高斯混合模型中分量的个数
采用BIC可以有效的选择高斯混合中的分量个数。理论上讲,它仅在近似状态下(即,如果有大量数据可用并假设数据实际上是由一个混合高斯模型生成)才能恢复模型的真实分量数。请注意,使用变分贝叶斯高斯混合 可避免指定高斯混合模型的分量数。
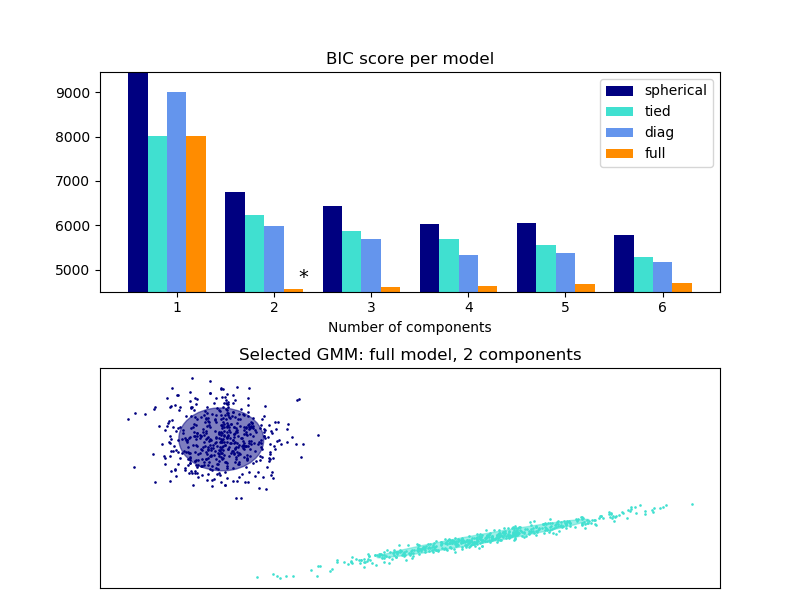 示例:
示例:
有关使用经典高斯混合执行模型选择的示例,请查阅 高斯混合模型选择
2.1.1.3. 估计算法期望最大化
从未标记的数据中学习高斯混合模型的主要困难在于,通常不知道哪个点来自哪个隐分量(如果可以得到这些信息,则很容易通过相应的数据点,拟合每个独立的高斯分布)。Expectation-maximization 是一种基于迭代来解决此问题的可靠统计算法。首先假设一个随机分量(随机地选取一个数据点为中心点,该点可以由k-means算法获得,也可以原点附近的正态分布点),并为每个点计算由模型的每个分量生成的概率。然后,调整模型参数以最大化模型生成这些参数的可能性。重复此过程可确保始终收敛到一个局部最优值。
2.1.2. 变分贝叶斯高斯混合
BayesianGaussianMixture对象是高斯混合模型的变体,使用变分推理算法实现。该API和 GaussianMixture 所定义的API类似。
2.1.2.1. 估计算法:变分推断
变分推理是期望最大化算法的扩展,它最大化了模型证据(包括先验)的下界,而不是数据的似然概率。变分方法背后的原理与期望最大化相同(两者都是迭代算法,在找到每种模型混合生成的每个点的概率与将模型拟合到这些分配的点之间交替进行),但变分方法通过整合来自先验分布的信息添加正则化。这避免了通常在期望最大化算法中发现的奇异性,但也为模型引入了一些细微的偏差。推理过程通常明显变慢,但一般也不会慢到无法使用。
由于其贝叶斯性质,变分算法需要比期望最大化更多的超参数,其中最重要的是浓度参数weight_concentration_prior。为先验浓度指定一个较低的值将使模型将大部分权重分配给少数分量,这样其余组分的权重就接近于零。先验的高浓度值将允许混合中有更多的分量在混合模型中都有相当比例的权重。
BayesianGaussianMixture类的参数实现权重分布提出了两种先验类型:具有Dirichlet distribution(狄利克雷分布)的有限混合模型和具有 Dirichlet Process(狄利克雷过程)的无限混合模型。在实践中,Dirichlet Process推理算法是近似的,并使用具有固定最大分量数的截断分布(称为“Stick-breaking representation”)。实际使用的分量数量几乎总是依赖数据。
下图比较了不同类型的加权浓度先验(参数weight_concentration_prior_type)对比不同类型的加权浓度先验所获得的结果weight_concentration_prior。在这里,我们可以看到weight_concentration_prior参数的值对获得的有效激活的分量数有很大的影响。还可以注意到,当先验类型为'dirichlet_distribution'时,先验浓度权重较大会导致权重更均匀,而'dirichlet_process'类型(默认类型)不一定如此。

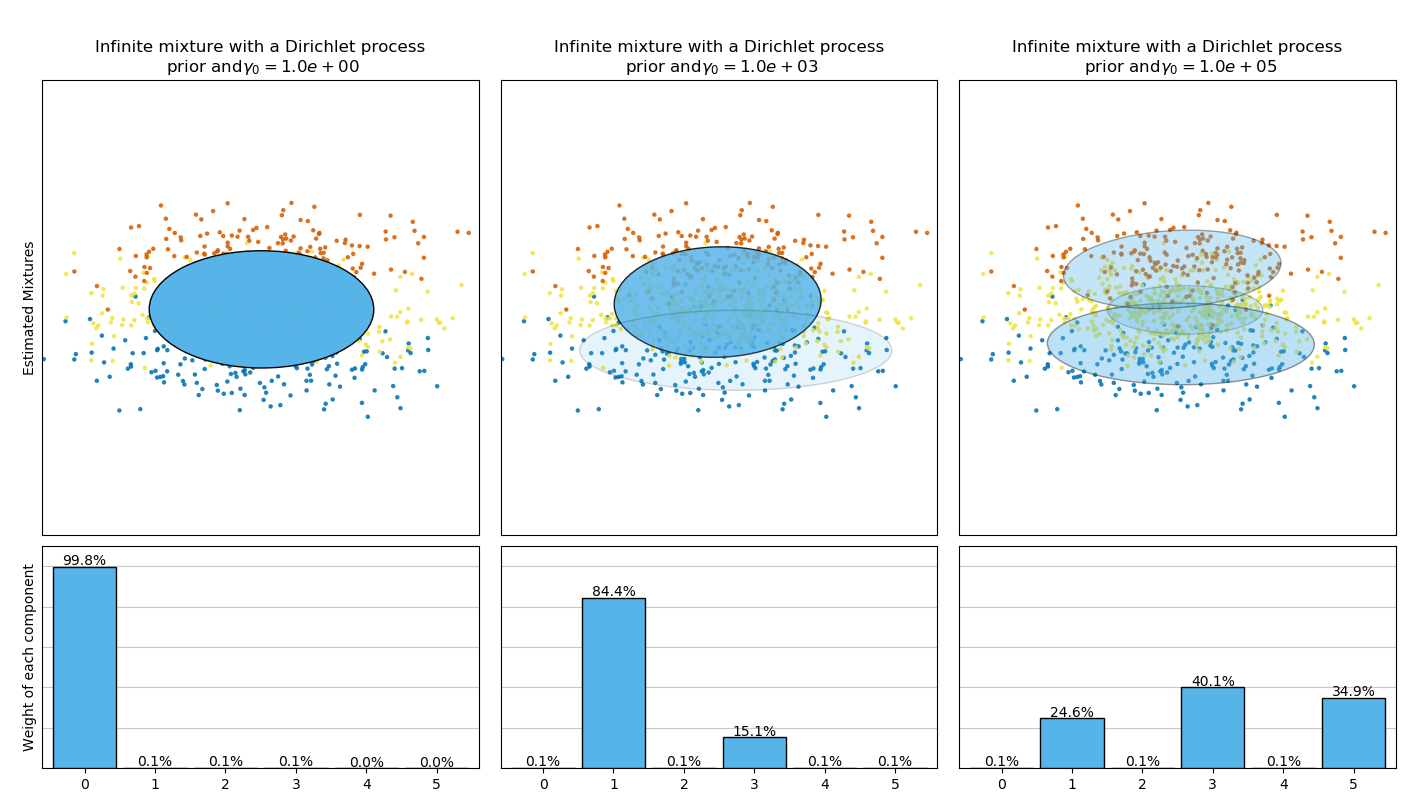 下面的示例将具有固定数量分量的高斯混合模型与先验Dirichlet process prior(狄利克雷过程先验)的变分高斯混合模型进行了比较。在这里,一个经典的高斯混合模型在由2个聚类组成的数据集,具有5个分量。我们可以看到具有Dirichlet过程先验的变分高斯混合模型能够将自身限制为仅2个分量,而高斯混合将数据与具有固定数量的分量拟合时用户必须事先设置固定数量的分量。在该示例中,用户选择
下面的示例将具有固定数量分量的高斯混合模型与先验Dirichlet process prior(狄利克雷过程先验)的变分高斯混合模型进行了比较。在这里,一个经典的高斯混合模型在由2个聚类组成的数据集,具有5个分量。我们可以看到具有Dirichlet过程先验的变分高斯混合模型能够将自身限制为仅2个分量,而高斯混合将数据与具有固定数量的分量拟合时用户必须事先设置固定数量的分量。在该示例中,用户选择 n_components=5,与真正的试用数据集(toy dataset)的生成分量数量不符。很容易注意到, 狄利克雷过程先验的变分高斯混合模型可以采取保守的策略,仅拟合生成一个分量。
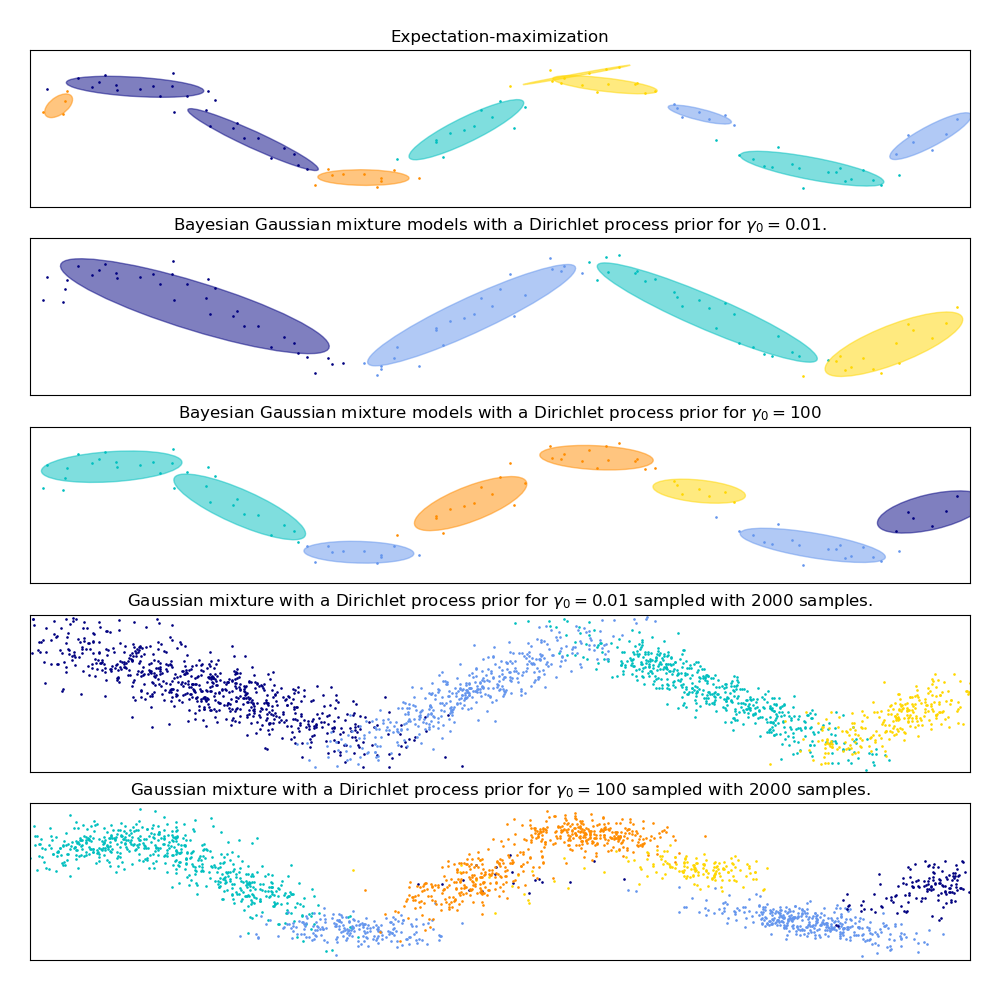
 在下图中,我们将拟合一个并不能被高斯混合模型很好描述的数据集。 调整
在下图中,我们将拟合一个并不能被高斯混合模型很好描述的数据集。 调整 BayesianGaussianMixture 类的参数 weight_concentration_prior ,这个参数决定了用来拟合数据的分量数量。我们在最后两个图上展示了从两个混合结果中产生的随机抽样。
 示例:
示例:
一个用 GaussianMixture和BayesianGaussianMixture绘制置信椭圆体的示例, 请参考 高斯混合模型椭球高斯混合模型正弦曲线 这个示例展示了用 GaussianMixture和BayesianGaussianMixture来拟合正弦波。一个使用不同的 weight_concentration_prior_type以不同的weight_concentration_prior参数值的 BayesianGaussianMixture 来绘制置信椭圆体的示例。 请参考 变分贝叶斯-高斯混合模型的浓度先验类型分析
2.1.2.2. BayesianGaussianMixture 下的变分推理的优缺点
2.1.2.2.1. 优点
自动选择: 当 weight_concentration_prior足够小且n_components大于模型所需要的值时,变分贝叶斯混合模型自然会倾向于将某些混合权重值设置为接近零。 这样就可以让模型自动选择合适数量的有效分量。过程仅需要提供分量的数量上限。但是注意,“理想” 的激活分量数量是针对特定应用的,在设置数据挖掘参数时通常并不明确。对参数数量的敏感度较低: 与有限模型不同,有限模型几乎总是尽可能多地使用分量,因此对于不同数量的分量将产生完全不同的解决方案, 而Dirichlet过程的先验的变分推理( weight_concentration_prior_type='dirichlet_process')的输出并不总随参数的变化而变化, 因此该变分推理更加稳定且需要更少的调优。正则化: 由于结合了先验信息,因此变分的解比期望最大化(EM)的解有更少的病理特征。
2.1.2.2.2. 缺点
速度: 变分推理所需要的额外参数化使推理变慢,尽管幅度不大。 超参数: 该算法需要一个额外的超参数,可能需要通过交叉验证进行实验调优的超参数。 偏差: 在推理算法中(以及在使用Dirichlet过程中)存在许多隐含的偏差, 并且只要这些偏差与数据之间不匹配,就有可能使用有限模型来拟合出更好的模型。
2.1.2.3. The Dirichlet Process(狄利克雷过程)
本文描述了狄利克雷过程混合的变分推理算法。狄利克雷过程是在分区数无限、无限大的聚类上的先验概率分布。与有限高斯混合模型相比,变分技术使我们在推理时间上几乎不受惩罚的纳入了高斯混合模型的先验结构。
一个重要的问题是,Dirichlet过程如何使用无穷多的聚类数,并且结果仍然保持一致。虽然本手册没有做出完整的解释,但你可以参考 stick breaking process来帮助理解它。是狄利克雷过程的衍生。我们从一个单位长度的 stick 开始,在每一步都折断剩下的 stick 的一部分。每一次,我们把 stick 的长度联想成所有点里落入一组混合的点的比例。 最后,为了表示无限混合,我们把 stick 的最后剩余部分联想成没有落入其他组的点的比例。每段的长度是一个随机变量, 其概率与浓度参数成正比。较小的浓度值将把单位长度分成更大的 stick 段(定义更集中的分布)。浓度值越大, stick 段越小(即增加非零权重的分量数量)。
在对该无限混合模型进行有限近似的情形下狄利克雷过程的变分推理技术仍然可以使用。我们不必事先指定想要的分量数量,只需要指定浓度参数和混合分量数的上界(假定上界高于“真实”的分量数,这仅仅影响算法复杂度,而不是实际使用的分量数量)。




