Search

Search Results

Search finished, found 840 page(s) matching the search query.

• sklearn.svm.NuSVC
  ```python class sklearn.svm.NuSVC(*, nu=0.5, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrin
• sklearn.tree.DecisionTreeRegressor
  ```python class sklearn.tree.DecisionTreeRegressor(*, criterion='mse', splitter='best', max_depth=No
• sklearn.utils.validation.check_symmetric
  ```python sklearn.utils.validation.check_symmetric(array, *, tol=1e-10, raise_warning=True, raise_e
• sklearn.gaussian_process.PairwiseKernel
  ``` class sklearn.gaussian_process.kernels.PairwiseKernel(gamma=1.0, gamma_bounds=(1e-05, 100000.0),
• 3.1 交叉验证：评估模型表现
  ​ 通过对预测函数参数的训练，并在相同的数据集上进行测试，是一个错误的方法论：如果一个模型对相同样本标签进行训练和测试，模型的得分会很高，但在实验数据上的表现会很差，这种情况被称为过拟合。为了避免过
• 正态和收缩线性判别分析在分类中的应用
  显示收缩如何改善分类。 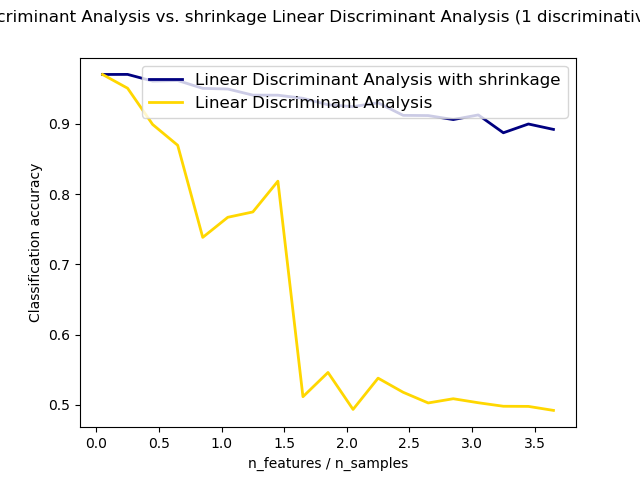 ```python import numpy as np i
• 决策树回归
  用决策树进行一维的回归。 利用[决策树](https://scikit-learn.org.cn/view/89.html)对正弦曲线进行加噪观测拟合。因此，它学习了近似正弦曲线的局部线性回归。
• 特征聚集与单变量选择
  此示例比较了2种降维策略： - 基于Anova的单变量特征选择 - 基于区域层次聚类的特征聚集 在一个以BayesianRidge作为有监督估计器的回归问题中，对这两种方法进行了比较。
• Ledoit-Wolf vs OAS估计器
  常用的协方差极大似然估计可以用shrinkage进行正则化。Ledoit和Wolf提出了一个计算渐近最优shrinkage 参数(最小MSE准则)的封闭公式，得到了Ledoit-Wolf协方差估计。
• 1.13 特征选择
  [`sklearn.feature_selection`](http://scikit-learn.jg.com.cn/lists/3.html#sklearn.feature_selection%E
• 2.5. 分解成分中的信号（矩阵分解问题）
  ## 2.5.1. 主成分分析（PCA） ### 2.5.1.1. 准确的PCA和概率解释（Exact PCA and probabilistic interpretation） 主成分分析（PC
• 6.5 无监督降维
  如果数据集的特征数量很多，则在进行有监督的步骤之前先通过无监督的步骤来减少特征数可能会很有用。许多 [无监督学习](https://scikit-learn.org.cn/lists/11.html)
• 核PCA
  此示例表明，核主成分分析能够找到数据的投影，从而使数据线性可分。 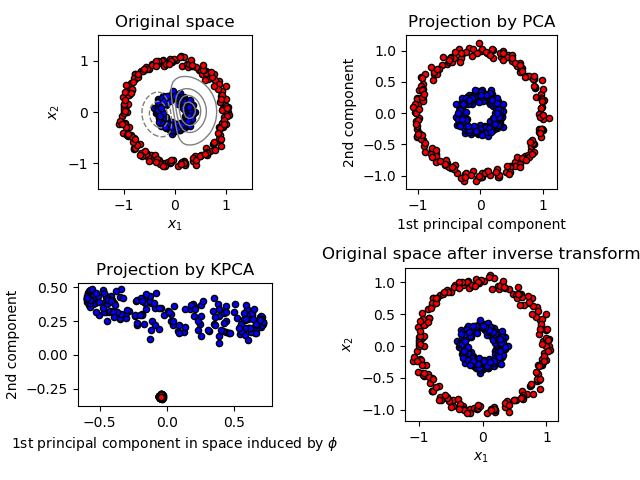 ```python pr
• 树集成的特征转换
  将你的特征转换成一个更高的空间，稀疏的空间。然后根据这些特征建立线性模型。 首先，在训练集上拟合一个树的集成(完全随机树、随机森林或梯度提升树)。然后，在一个新的特征空间中，为集合中的每一棵树分
• 维基百科主特征向量
  判断图中顶点相对重要性的一种经典方法是计算邻接矩阵的主特征向量，以便将第一个特征向量的分量作为中心分数分配给每个顶点： https://en.wikipedia.org/wiki/Eigenve

首页上一页32333435363738下一页末页