不同核的高斯过程的先验和后验示例¶
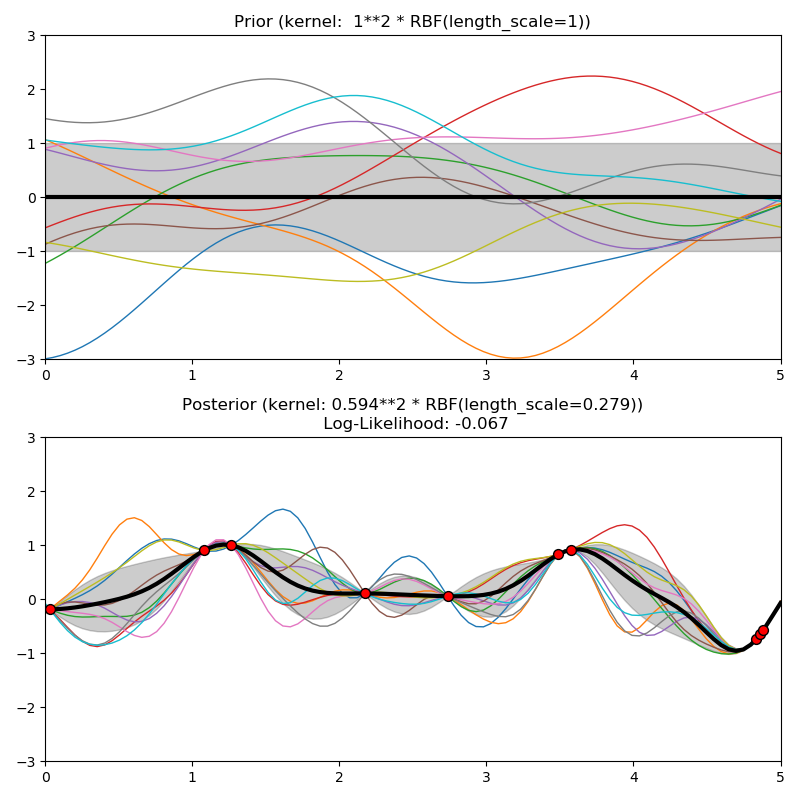
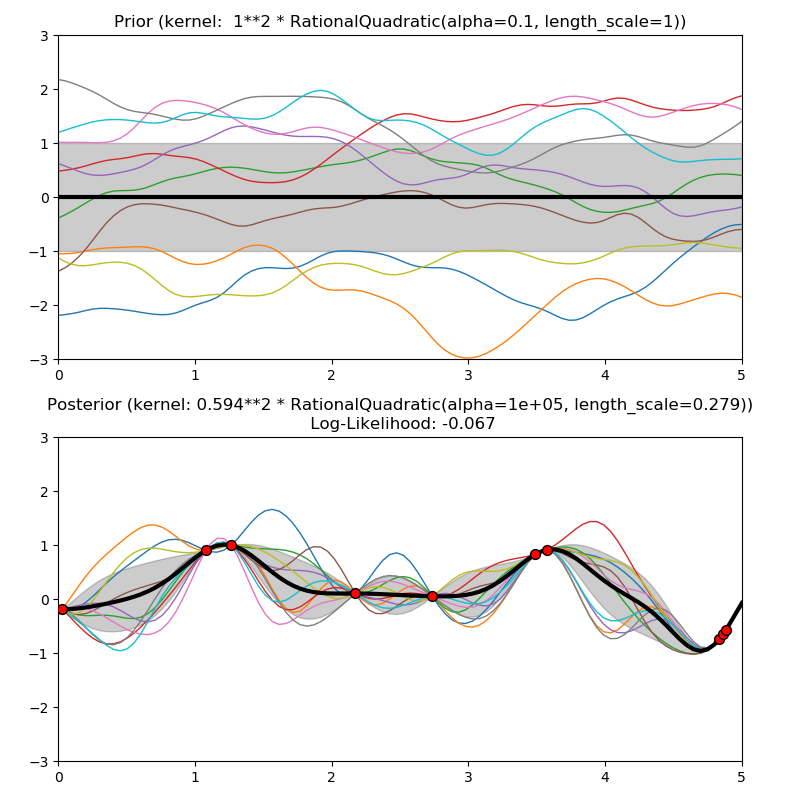
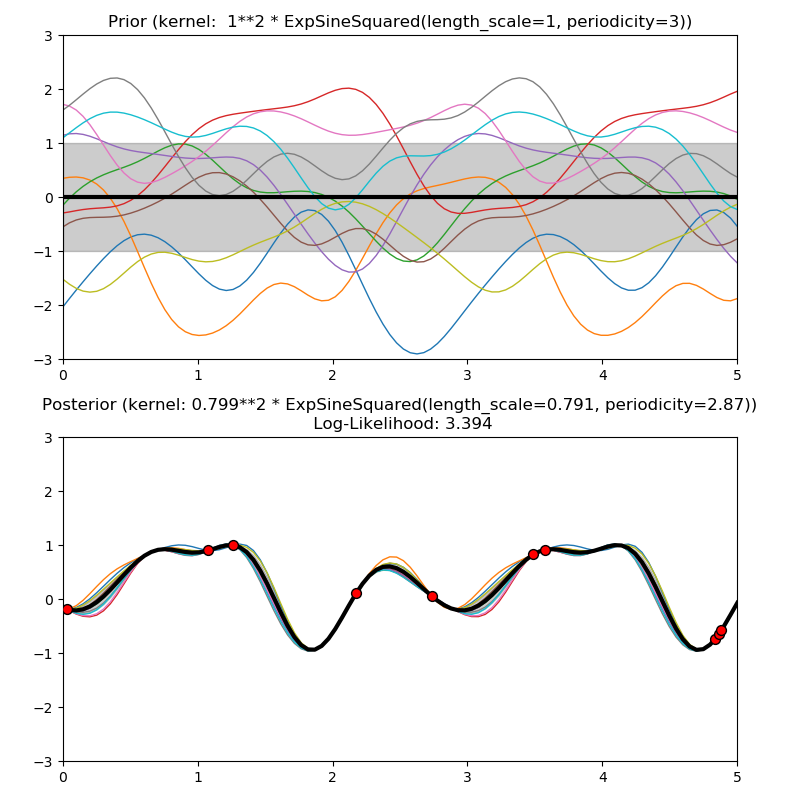
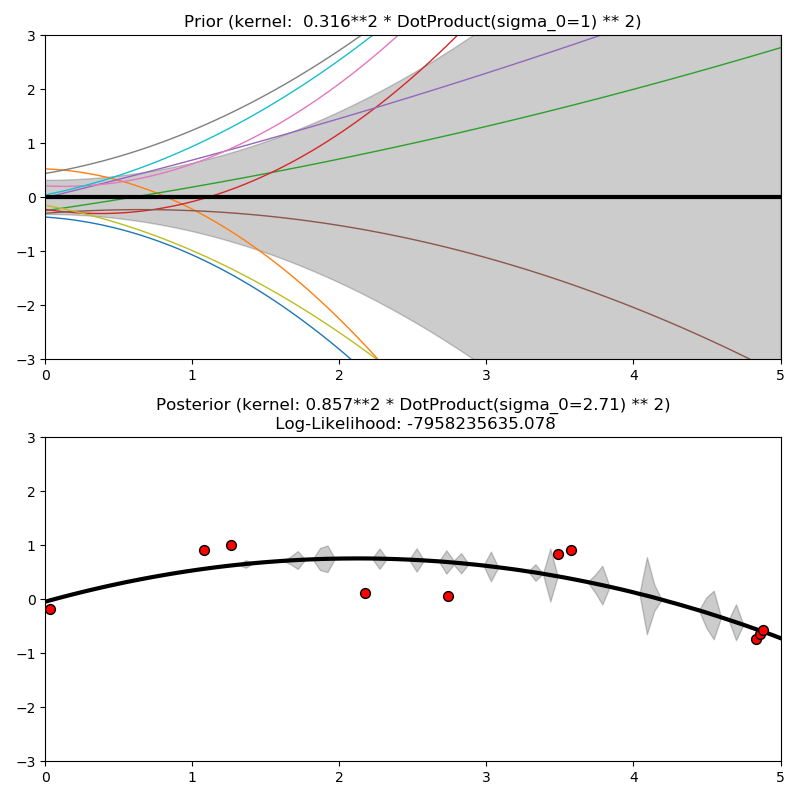
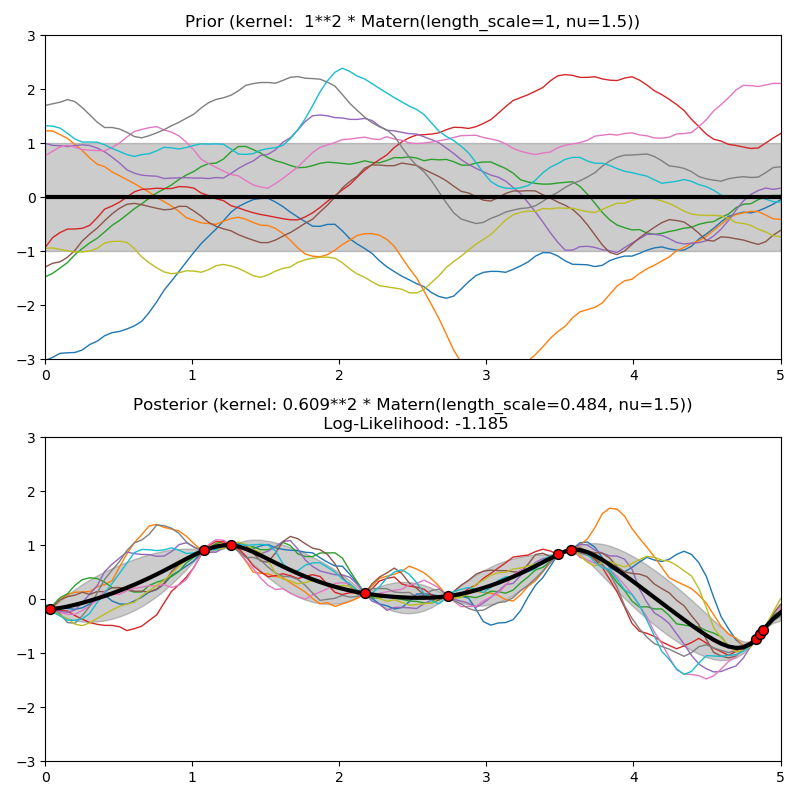
这个例子说明了具有不同内核的GPR的先验和后验。平均值,标准差,和10个样本都显示对于先验和后验。
/home/circleci/project/sklearn/gaussian_process/_gpr.py:504: ConvergenceWarning: lbfgs failed to converge (status=2):
ABNORMAL_TERMINATION_IN_LNSRCH.
Increase the number of iterations (max_iter) or scale the data as shown in:
https://scikit-learn.org/stable/modules/preprocessing.html
_check_optimize_result("lbfgs", opt_res)
/home/circleci/project/sklearn/gaussian_process/_gpr.py:370: UserWarning: Predicted variances smaller than 0. Setting those variances to 0.
warnings.warn("Predicted variances smaller than 0. "
print(__doc__)
# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import (RBF, Matern, RationalQuadratic,
ExpSineSquared, DotProduct,
ConstantKernel)
kernels = [1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0)),
1.0 * RationalQuadratic(length_scale=1.0, alpha=0.1),
1.0 * ExpSineSquared(length_scale=1.0, periodicity=3.0,
length_scale_bounds=(0.1, 10.0),
periodicity_bounds=(1.0, 10.0)),
ConstantKernel(0.1, (0.01, 10.0))
* (DotProduct(sigma_0=1.0, sigma_0_bounds=(0.1, 10.0)) ** 2),
1.0 * Matern(length_scale=1.0, length_scale_bounds=(1e-1, 10.0),
nu=1.5)]
for kernel in kernels:
# Specify Gaussian Process
gp = GaussianProcessRegressor(kernel=kernel)
# Plot prior
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
X_ = np.linspace(0, 5, 100)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
alpha=0.2, color='k')
y_samples = gp.sample_y(X_[:, np.newaxis], 10)
plt.plot(X_, y_samples, lw=1)
plt.xlim(0, 5)
plt.ylim(-3, 3)
plt.title("Prior (kernel: %s)" % kernel, fontsize=12)
# Generate data and fit GP
rng = np.random.RandomState(4)
X = rng.uniform(0, 5, 10)[:, np.newaxis]
y = np.sin((X[:, 0] - 2.5) ** 2)
gp.fit(X, y)
# Plot posterior
plt.subplot(2, 1, 2)
X_ = np.linspace(0, 5, 100)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
alpha=0.2, color='k')
y_samples = gp.sample_y(X_[:, np.newaxis], 10)
plt.plot(X_, y_samples, lw=1)
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.xlim(0, 5)
plt.ylim(-3, 3)
plt.title("Posterior (kernel: %s)\n Log-Likelihood: %.3f"
% (gp.kernel_, gp.log_marginal_likelihood(gp.kernel_.theta)),
fontsize=12)
plt.tight_layout()
plt.show()
脚本的总运行时间:(0分1.299秒)




