1.3 内核岭回归¶

内核岭回归(Kernel ridge regression (KRR)) [M2012] , 是组合使用了内核技巧和岭回归(进行了l2正则化的最小二乘法)。因此，它所学习到的在空间中不同的线性函数是由不同的内核和数据所导致的。对于非线性的内核，它与原始空间中的非线性函数相对应。

通过 KernelRidge学习到的模型与支持向量回归（SVR）是一样的。但是他们使用了不同的损失函数：内核岭回归(KRR)使用了均方误差损失(squared error loss), 而支持向量回归(support vector regression， SVR)使用了 -insensitive损失， 两则都使用了l2进行正则化。与[`SVR`](https://scikit-learn.org.cn/view/782.html)相反， [`KernelRidge`](https://scikit-learn.org.cn/view/377.html) 的拟合可以以封闭形式进行，而且对于中等大小的数据集来说通常更快。在另一方面， 它所学习的模型是非稀疏的，因此在预测时间上来看比支持向量回归(SVR)要慢, 而支持向量回归对于会学习一个稀疏的模型。

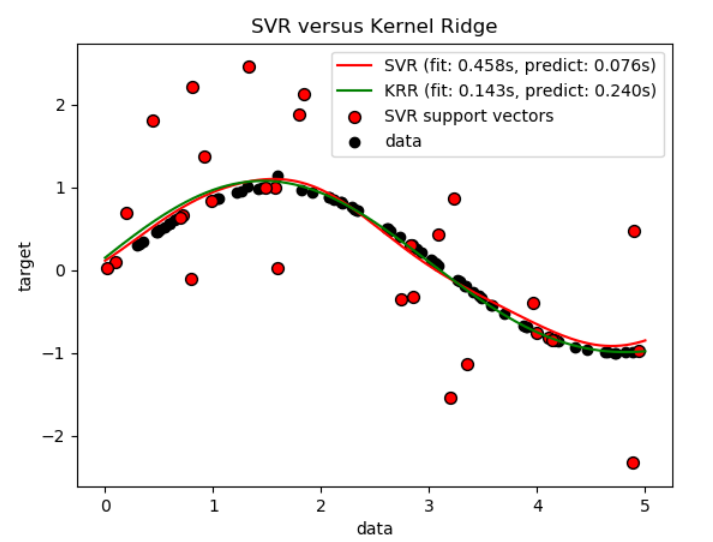
下图比较了人造数据集上的KernelRidge和 SVR，这是一个包含正弦函数和每五个数据点就加上一个强噪声的数据集。下面绘制了 KernelRidge和SVR的模型， 通过网格搜索优化了（高斯**）**径向基函数核函数（RBF核）的复杂度、正则化和带宽。学习的函数是非常相似的；然而，都是网格搜索情况下， 拟合KernelRidge大约比拟合SVR快7倍。然而，100000目标值的预测要快三倍多，因为它已经学习了一个稀疏模型，仅使用100个训练数据点的1/3作为支持向量。

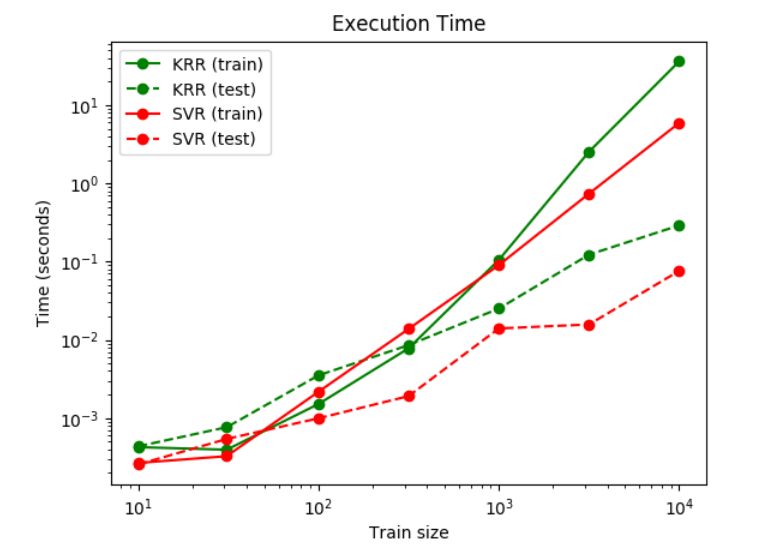
下一个图比较了在不同大小的训练集上KernelRidge和SVR的拟合和预测时间。对于中等训练集，拟合KernelRidge比 SVR快(小于1000个样本)；然而，对于更大的训练集，SVR通常更好。关于预测的时间，在所有大小的训练集上SVR比KernelRidge更快，因为学习SVR得到的是稀疏的解。请注意，稀疏的程度和预测的时间取决于SVR的参数ϵ和C；ϵ=0将对应于稠密模型。

参考

[2012]"机器学习：概率视角"Murphy, K. P. - chapter 14.4.3, pp. 492-493, The MIT Press, 2012