不同度量的聚集聚类¶

演示不同度量对分层聚类的影响。

该示例的设计表明了选择不同度量标准的效果。它应用于波形，可视为高维向量。实际上，度量之间的差异通常在高维(特别是欧几里得度量和城市街道度量)中更为明显。

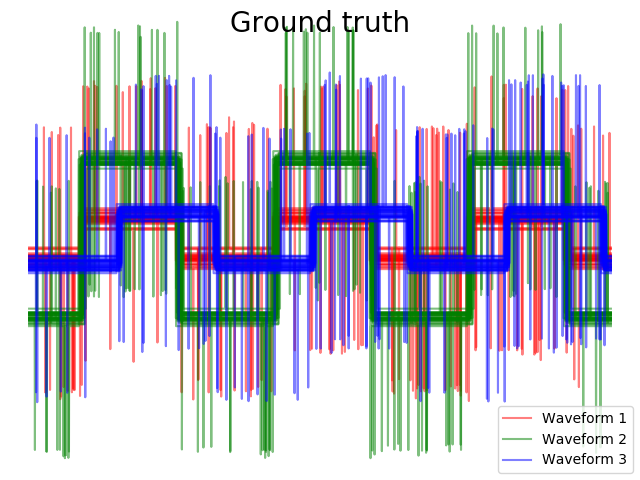
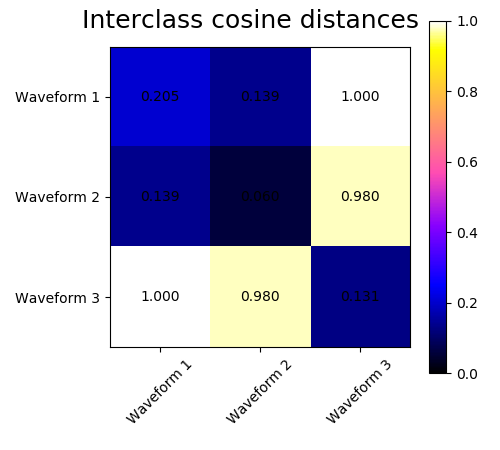
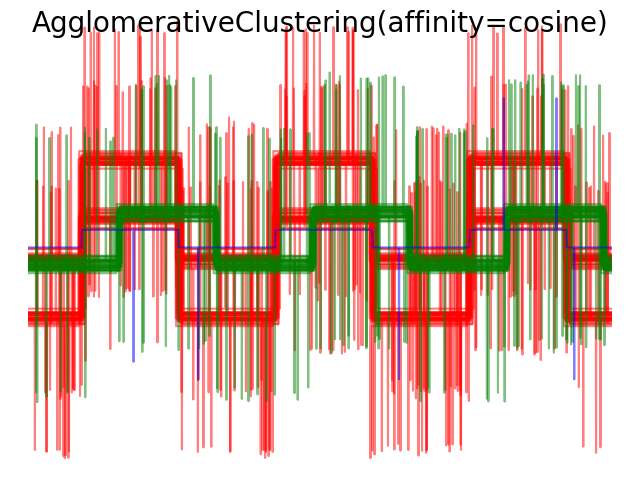
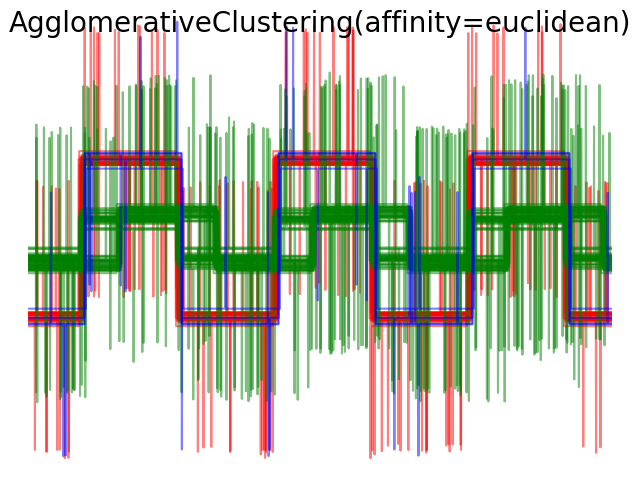
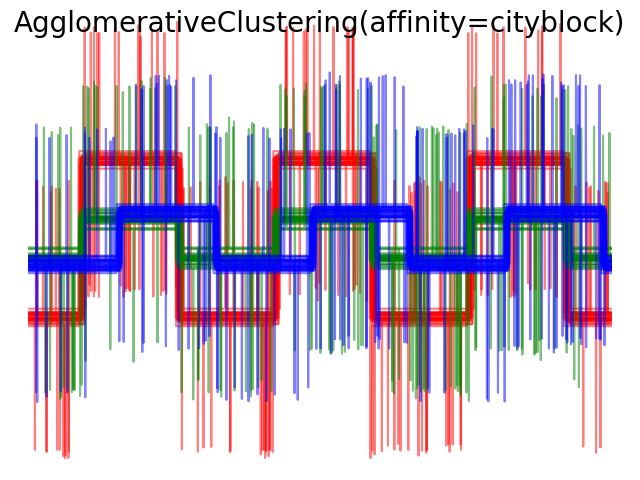
我们从三组波形中生成数据。两种波形(波形1和波形2)是成比例的。余弦距离不受数据缩放的影响，因此无法区分这两种波形。因此，即使没有噪声，使用这个距离的聚类也不会分离出波形1和2。

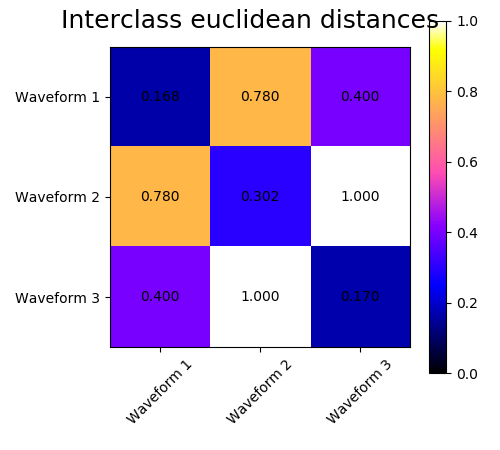
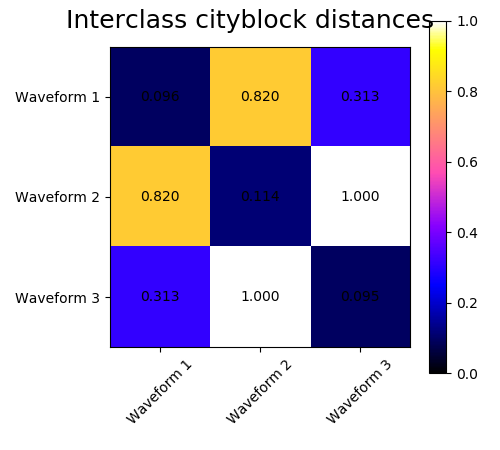
我们在这些波形中加入观测噪声。我们产生非常稀疏的噪声：只有6%的时间点含有噪声。因此，这种噪声的L1范数(即“街道”距离)比它的L2范数(“欧几里得”距离)要小得多。这可以在类间距离矩阵上看到：描述类的扩展的对角线上的值对于欧氏距离要比街道距离大得多。当我们将聚类应用于数据时，我们发现聚类反映了距离矩阵中的内容。实际上，对于欧氏距离，由于噪声的影响，类之间是不分离的，因此聚类不分离波形。对于街道距离，分离良好，波形类恢复。最后，余弦距离在所有波形1和2都不分开，因此聚类将它们放在同一簇中。

# Author: Gael Varoquaux
# License: BSD 3-Clause or CC-0

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distances

np.random.seed(0)

# Generate waveform data
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)


def sqr(x):
    return np.sign(np.cos(x))

X = list()
y = list()
for i, (phi, a) in enumerate([(.5, .15), (.5, .6), (.3, .2)]):
    for _ in range(30):
        phase_noise = .01 * np.random.normal()
        amplitude_noise = .04 * np.random.normal()
        additional_noise = 1 - 2 * np.random.rand(n_features)
        # Make the noise sparse
        additional_noise[np.abs(additional_noise) < .997] = 0

        X.append(12 * ((a + amplitude_noise)
                 * (sqr(6 * (t + phi + phase_noise)))
                 + additional_noise))
        y.append(i)

X = np.array(X)
y = np.array(y)

n_clusters = 3

labels = ('Waveform 1', 'Waveform 2', 'Waveform 3')

# Plot the ground-truth labelling
plt.figure()
plt.axes([0, 0, 1, 1])
for l, c, n in zip(range(n_clusters), 'rgb',
                   labels):
    lines = plt.plot(X[y == l].T, c=c, alpha=.5)
    lines[0].set_label(n)

plt.legend(loc='best')

plt.axis('tight')
plt.axis('off')
plt.suptitle("Ground truth", size=20)


# Plot the distances
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    avg_dist = np.zeros((n_clusters, n_clusters))
    plt.figure(figsize=(5, 4.5))
    for i in range(n_clusters):
        for j in range(n_clusters):
            avg_dist[i, j] = pairwise_distances(X[y == i], X[y == j],
                                                metric=metric).mean()
    avg_dist /= avg_dist.max()
    for i in range(n_clusters):
        for j in range(n_clusters):
            plt.text(i, j, '%5.3f' % avg_dist[i, j],
                     verticalalignment='center',
                     horizontalalignment='center')

    plt.imshow(avg_dist, interpolation='nearest', cmap=plt.cm.gnuplot2,
               vmin=0)
    plt.xticks(range(n_clusters), labels, rotation=45)
    plt.yticks(range(n_clusters), labels)
    plt.colorbar()
    plt.suptitle("Interclass %s distances" % metric, size=18)
    plt.tight_layout()


# Plot clustering results
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    model = AgglomerativeClustering(n_clusters=n_clusters,
                                    linkage="average", affinity=metric)
    model.fit(X)
    plt.figure()
    plt.axes([0, 0, 1, 1])
    for l, c in zip(np.arange(model.n_clusters), 'rgbk'):
        plt.plot(X[model.labels_ == l].T, c=c, alpha=.5)
    plt.axis('tight')
    plt.axis('off')
    plt.suptitle("AgglomerativeClustering(affinity=%s)" % metric, size=20)


plt.show()

脚本的总运行时间：(0分1.504秒)

Download Python source code:plot_agglomerative_clustering_metrics.py

Download Jupyter notebook:plot_agglomerative_clustering_metrics.ipynb