在鸢尾花数据集中绘制不同的SVM分类器¶
在鸢尾花数据集的二维投影上比较不同的线性支持向量机分类器。我们仅考虑此数据集的前两个特征:
花萼长度
花萼宽度
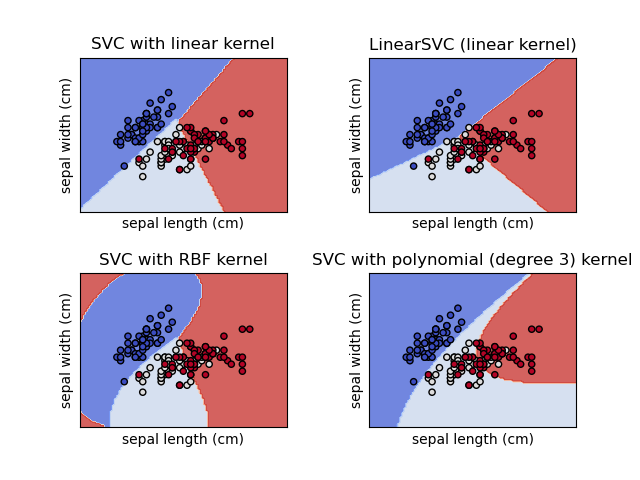
此案例会说明如何绘制具有不同核函数的四个SVM分类器的决策平面。
线性模型LinearSVC()和SVC(kernel ='linear')得出的决策边界略有不同。 这可能是由于以下差异造成的:
LinearSVC()最小化平方hinge损失,而SVC最小化普通的hinge损失。
LinearSVC()使用“一对全(One-vs-All)”(也称为“一对多 One-vs-Rest”)多类归约,而SVC使用“一对一(One-vs-One)”多类归约。
两种线性模型都有线性决策边界(对多分类而言,相交的超平面),而非线性内核模型(多项式或高斯RBF)则具有更灵活的非线性决策边界,其形状取决于内核的种类及其参数。
注意:
虽然为玩具(toy)二维数据集绘制分类器的决策函数可以帮助直观了解各个核函数的表达能力,但请注意,这些直觉并不总是会推广到更现实的高维问题。
输入:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
def make_meshgrid(x, y, h=.02):
"""创建要绘制的点网格
参数
----------
x: 创建网格x轴所需要的数据
y: 创建网格y轴所需要的数据
h: 网格大小的可选大小,可选填
返回
-------
xx, yy : n维数组
"""
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
"""绘制分类器的决策边界。
参数
----------
ax: matplotlib子图对象
clf: 一个分类器
xx: 网状网格meshgrid的n维数组
yy: 网状网格meshgrid的n维数组
params: 传递给contourf的参数字典,可选填
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
# 导入数据以便后续使用
iris = datasets.load_iris()
# 采用前两个特征。我们可以通过使用二维数据集来避免使用切片。
X = iris.data[:, :2]
y = iris.target
# 我们创建一个SVM实例并拟合数据。由于要绘制支持向量,因此我们不缩放数据
C = 1.0 # SVM正则化参数
models = (svm.SVC(kernel='linear', C=C),
svm.LinearSVC(C=C, max_iter=10000),
svm.SVC(kernel='rbf', gamma=0.7, C=C),
svm.SVC(kernel='poly', degree=3, gamma='auto', C=C))
models = (clf.fit(X, y) for clf in models)
# 为图像设置标题
titles = ('SVC with linear kernel',
'LinearSVC (linear kernel)',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel')
# 设置一个2x2结构的画布
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
for clf, title, ax in zip(models, titles, sub.flatten()):
plot_contours(ax, clf, xx, yy,
cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('Sepal length')
ax.set_ylabel('Sepal width')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()
脚本的总运行时间:(0分钟0.570秒)




