缩放SVC的正则化参数¶
这个案例展示了当我们使用支持向量机做分类时,对正则化参数进行缩放时的效果。在进行支持向量机分类时,我们对以下等式的风险最小化很感兴趣:
其中:
被用来设置正则项的数量 是样本和模型参数的损失函数 是模型参数的惩罚函数
如果我们将损失函数视为每个样本的个体误差,那么随着我们添加更多样本,数据拟合项或每个样本的误差之和将增加。但是,惩罚项却不会增加。
例如,当使用交叉验证来设置C的正则化量时,在主要问题(未进行交叉验证的全部数据集)和交叉验证过程中较小的问题(使用交叉验证分割后较小的数据集)之间将存在不同数量的样本。
由于损失函数取决于样本量,后者将影响C的选定值。现在出现的问题是,如何最佳地调整C以考虑不同数量的训练样本?
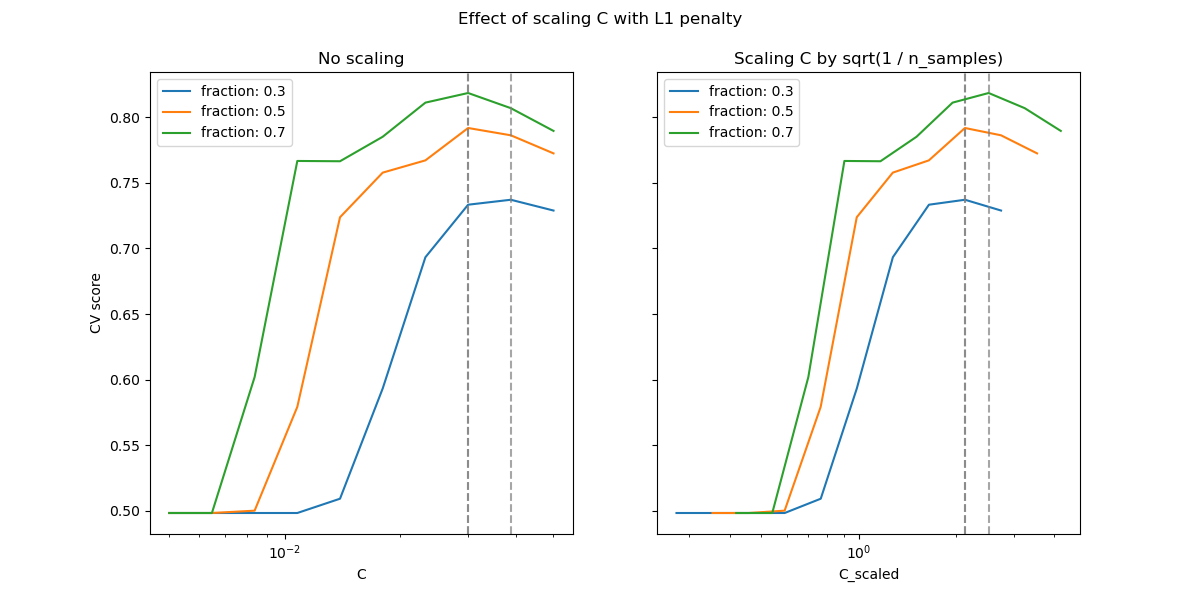
下图用于说明在使用l1罚分和l2罚分的情况下,缩放C以补偿样本数量变化的效果。
L1惩罚项的情况
在l1的情况下,理论认为由于l1的偏差,预测一致性(即,在给定的假设下,估算器能够学会预测并建立出一个知道数据真实分布的模型)是不可能的。但是,理论也确实认为,可以通过缩放来在找到正确的非零参数集及其符号方面实现模型一致性。
L2惩罚项的情况
理论认为,为了实现预测的一致性,惩罚参数应随着样本数量的增长而保持恒定。
模拟
针对生成的数据集的几个不同部分,本案例在下面两张图绘制了的值(X轴)及交叉验证分数(y轴)。
如第一个图所示,在L1的情况下,当我们依照样本量对进行缩放时,交叉验证错误和测试错误有极高的关联性。
在L2的情况下,当不对进行缩放时结果是最好的。
注意:
两个图像使用了不同的数据集。这样做的理由是:L1惩罚项实际上在稀疏矩阵上效果更好,而L2更适合于不稀疏的矩阵。

输入:
# 作者: Andreas Mueller <amueller@ais.uni-bonn.de>
# Jaques Grobler <jaques.grobler@inria.fr>
# 执照: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import GridSearchCV
from sklearn.utils import check_random_state
from sklearn import datasets
rnd = check_random_state(1)
# 设置数据集
n_samples = 100
n_features = 300
# L1情况下使用的数据集(仅有5个信息特征)
X_1, y_1 = datasets.make_classification(n_samples=n_samples,
n_features=n_features, n_informative=5,
random_state=1)
# L2情况下使用的数据集:非稀疏,但有更少的特征
y_2 = np.sign(.5 - rnd.rand(n_samples))
X_2 = rnd.randn(n_samples, n_features // 5) + y_2[:, np.newaxis]
X_2 += 5 * rnd.randn(n_samples, n_features // 5)
clf_sets = [(LinearSVC(penalty='l1', loss='squared_hinge', dual=False,
tol=1e-3),
np.logspace(-2.3, -1.3, 10), X_1, y_1),
(LinearSVC(penalty='l2', loss='squared_hinge', dual=True),
np.logspace(-4.5, -2, 10), X_2, y_2)]
colors = ['navy', 'cyan', 'darkorange']
lw = 2
for clf, cs, X, y in clf_sets:
# 对每个回归器设置图像
fig, axes = plt.subplots(nrows=2, sharey=True, figsize=(9, 10))
for k, train_size in enumerate(np.linspace(0.3, 0.7, 3)[::-1]):
param_grid = dict(C=cs)
# 为了获得良好的曲线,我们需要进行大量的迭代以减小方差
grid = GridSearchCV(clf, refit=False, param_grid=param_grid,
cv=ShuffleSplit(train_size=train_size,
test_size=.3,
n_splits=250, random_state=1))
grid.fit(X, y)
scores = grid.cv_results_['mean_test_score']
scales = [(1, 'No scaling'),
((n_samples * train_size), '1/n_samples'),
]
for ax, (scaler, name) in zip(axes, scales):
ax.set_xlabel('C')
ax.set_ylabel('CV Score')
grid_cs = cs * float(scaler) # scale the C's
ax.semilogx(grid_cs, scores, label="fraction %.2f" %
train_size, color=colors[k], lw=lw)
ax.set_title('scaling=%s, penalty=%s, loss=%s' %
(name, clf.penalty, clf.loss))
plt.legend(loc="best")
plt.show()
脚本的总运行时间:(0分钟25.111秒)




