精确度-召回曲线¶
本案例用于展示评估分类器输出质量的精确度-召回曲线。
当样本的标签类别非常不平衡时,Precision-Recall是预测是否成功的有用度量。在信息检索中,精确度是结果相关性的度量,而召回率是返回多少真正相关的结果的度量。
精确度-召回曲线显示了不同阈值时精度和召回之间的权衡。曲线下的高区域代表高召回率和高精度,其中高精度与低假正率有关,高召回率与低假负率有关。两者的高分都表明分类器正在返回准确的结果(高精度),并且返回所有正样本的大部分(高召回率)。
召回率高但精度低的算法会返回许多结果,但是与训练标签相比,其大多数预测标签都不正确。具有高精度但召回率低的系统则相反,返回的结果很少,但是与训练标签相比,大多数预测标签都是正确的。具有高精度和高召回的理想系统将返回许多结果,并且所有结果均正确标记。
精度()的定义为:真阳性()的数量超过真阳性的数量加上假阳性()的数量。
召回()的定义为:真阳性的数量()超过真阳性的数量加上假阴性的数量()。
这些数量还与()分数相关,该分数定义为精确度和召回的调和平均值。
请注意,精度可能不会随召回而降低。精度的定义()表明,降低分类器的阈值可以通过增加返回的结果数来增加分母。如果先前将阈值设置得太高,则新结果可能都是真阳性,这将提高精度。如果先前的阈值大约正确或太低,则进一步降低阈值将引入误报,从而降低精度。
召回率被定义为,其中不取决于分类器阈值。这意味着降低分类器阈值可能会通过增加真实阳性结果的数量来增加召回率。降低阈值也可能使召回率保持不变,而精度会波动。
可以在绘图的阶梯区域中观察到召回率与精度之间的关系-在这些步骤的边缘,阈值的微小变化会显着降低精度,而召回率只有很小的提高。
平均精度(AP)总结了这样一个图,即在每个阈值处获得的精度的加权平均值,而前一个阈值的召回率增加用作权重:
其中和是第n个阈值的精度和召回率。一对被成为称为操作点(operating point)。
AP和操作点下的梯形区域(sklearn.metrics.auc)是汇总精确召回曲线的常见方法,可得出不同的结果。在用户指南中阅读更多内容。
精确召回曲线通常用于二分类中,以研究分类器的输出。为了将精确度调用曲线和平均精确度扩展到多类或多标签分类,必须对输出进行二值化。每个标签可以绘制一条曲线,但也可以通过将标签指示符矩阵的每个元素视为二进制预测(微平均)来绘制精确召回曲线。
注意,请同时查看:sklearn.metrics.average_precision_score,
sklearn.metrics.recall_score, sklearn.metrics.precision_score, sklearn.metrics.f1_score
在二分类情况下
1、创建样本数据
尝试区分鸢尾花数据集的前两个类。
from sklearn import svm, datasets
from sklearn.model_selection import train_test_split
import numpy as np
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 增加噪音特征
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
# 限制在前两个类别上,并且将数据分类为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X[y < 2], y[y < 2],
test_size=.5,
random_state=random_state)
# 创建一个简单的分类器
classifier = svm.LinearSVC(random_state=random_state)
classifier.fit(X_train, y_train)
y_score = classifier.decision_function(X_test)
2、计算平均精确度分数
from sklearn.metrics import average_precision_score
average_precision = average_precision_score(y_test, y_score)
print('Average precision-recall score: {0:0.2f}'.format(
average_precision))
输出:
Average precision-recall score: 0.88
3、绘制精确度-召回率曲线
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import plot_precision_recall_curve
import matplotlib.pyplot as plt
disp = plot_precision_recall_curve(classifier, X_test, y_test)
disp.ax_.set_title('2-class Precision-Recall curve: '
'AP={0:0.2f}'.format(average_precision))
输出:
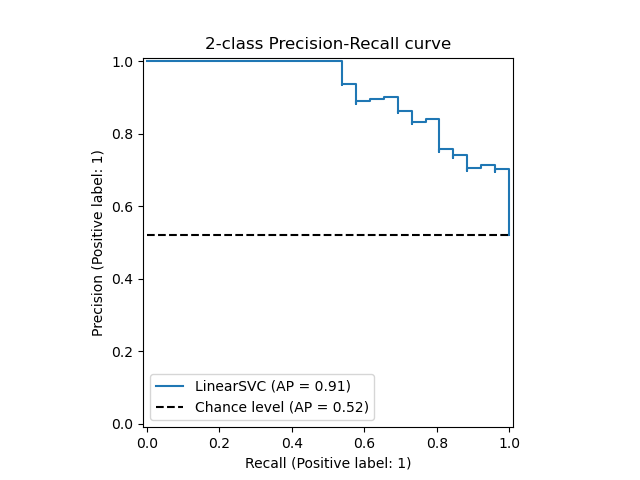
Text(0.5, 1.0, '2-class Precision-Recall curve: AP=0.88')
在多标签情况下
1、创造多标签数据,拟合并进行预测
我们创建了一个多标签数据集,以说明多标签设置中的精确度-召回率曲线。
from sklearn.preprocessing import label_binarize
# 使用label_binarize让数据成为类似多标签的设置
Y = label_binarize(y, classes=[0, 1, 2])
n_classes = Y.shape[1]
# 分割训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5,
random_state=random_state)
# 我们使用OneVsRestClassifier进行多标签预测
from sklearn.multiclass import OneVsRestClassifier
# 运行分类器
classifier = OneVsRestClassifier(svm.LinearSVC(random_state=random_state))
classifier.fit(X_train, Y_train)
y_score = classifier.decision_function(X_test)
2、多标签设置中的平均精度得分
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
# 对每个类别
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
precision[i], recall[i], _ = precision_recall_curve(Y_test[:, i],
y_score[:, i])
average_precision[i] = average_precision_score(Y_test[:, i], y_score[:, i])
# 一个"微观平均": 共同量化所有课程的分数
precision["micro"], recall["micro"], _ = precision_recall_curve(Y_test.ravel(),
y_score.ravel())
average_precision["micro"] = average_precision_score(Y_test, y_score,
average="micro")
print('Average precision score, micro-averaged over all classes: {0:0.2f}'
.format(average_precision["micro"]))
输出:
Average precision score, micro-averaged over all classes: 0.43
3、绘制微观平均下的精确召回曲线
plt.figure()
plt.step(recall['micro'], precision['micro'], where='post')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title(
'Average precision score, micro-averaged over all classes: AP={0:0.2f}'
.format(average_precision["micro"]))
输出:
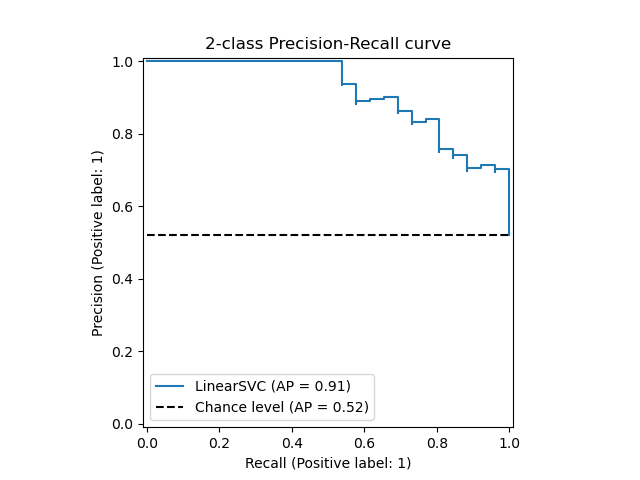
Text(0.5, 1.0, 'Average precision score, micro-averaged over all classes: AP=0.43')
4、为每个类和iso-f1曲线绘制Precision-Recall曲线
from itertools import cycle
# 设置绘图细节
colors = cycle(['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal'])
plt.figure(figsize=(7, 8))
f_scores = np.linspace(0.2, 0.8, num=4)
lines = []
labels = []
for f_score in f_scores:
x = np.linspace(0.01, 1)
y = f_score * x / (2 * x - f_score)
l, = plt.plot(x[y >= 0], y[y >= 0], color='gray', alpha=0.2)
plt.annotate('f1={0:0.1f}'.format(f_score), xy=(0.9, y[45] + 0.02))
lines.append(l)
labels.append('iso-f1 curves')
l, = plt.plot(recall["micro"], precision["micro"], color='gold', lw=2)
lines.append(l)
labels.append('micro-average Precision-recall (area = {0:0.2f})'
''.format(average_precision["micro"]))
for i, color in zip(range(n_classes), colors):
l, = plt.plot(recall[i], precision[i], color=color, lw=2)
lines.append(l)
labels.append('Precision-recall for class {0} (area = {1:0.2f})'
''.format(i, average_precision[i]))
fig = plt.gcf()
fig.subplots_adjust(bottom=0.25)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Extension of Precision-Recall curve to multi-class')
plt.legend(lines, labels, loc=(0, -.38), prop=dict(size=14))
plt.show()
输出:
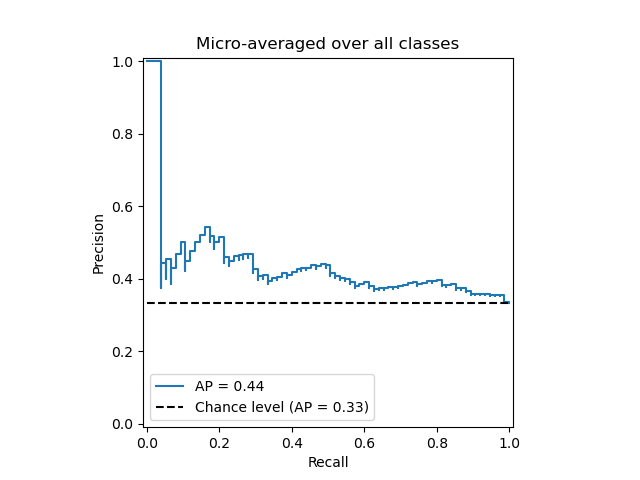
脚本的总运行时间:(0分钟0.330秒)




