绘制学习曲线¶
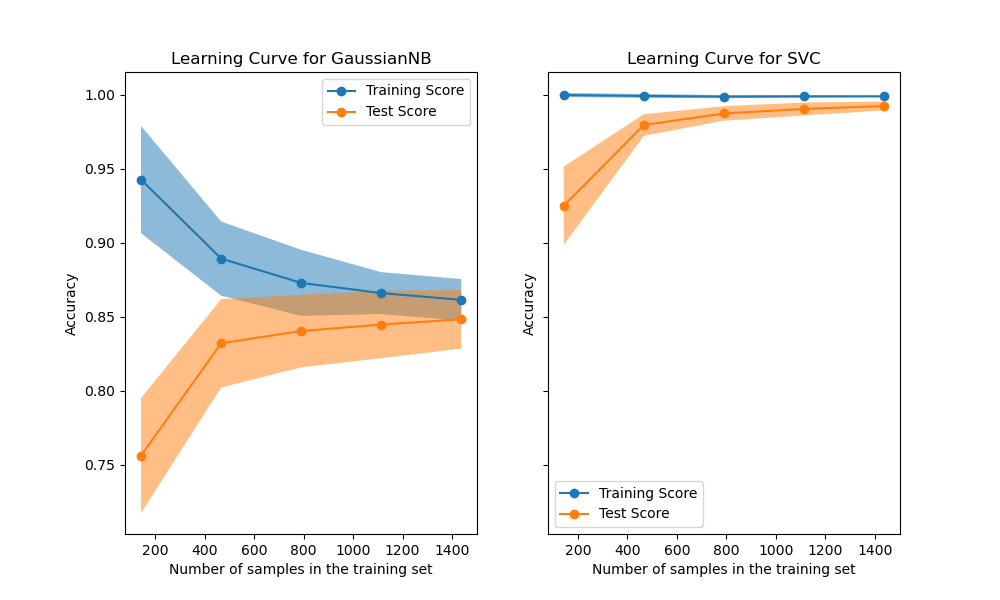
在第一列的第一行中,显示了手写数字数据集上朴素贝叶斯分类器的学习曲线。 请注意,训练分数和交叉验证分数最后都不太好。但是,这个曲线的形状经常会在更复杂的数据集中被找到:训练得分在开始时很高,然后降低,而交叉验证得分在开始时很低但是之后增加。在第二列的第一行中,我们看到带有RBF内核的SVM的学习曲线。我们可以清楚地看到,训练分数仍在最大值附近,并且可以通过增加训练样本来增加验证分数。第二行中的图显示了模型使用各种大小的训练数据集进行训练所需的时间。第三行中的图显示了每种训练规模需要多少时间来训练模型。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, axes=None, ylim=None, cv=None,
n_jobs=None, train_sizes=np.linspace(.1, 1.0, 5)):
"""
生成3个图:测试和训练学习曲线,训练样本与拟合时间曲线,拟合时间与得分曲线。
参数
----------
estimator : 实现“ fit”和“ predict”方法的对象类型
每次验证都会克隆的该类型的对象。
title : 字符串
图表标题。
X : 类数组,结构为(n_samples,n_features)
训练向量,其中n_samples是样本数,n_features是特征的数量。
y : 类数组,结构为(n_samples)或(n_samples,n_features),可选
相对于X的目标进行分类或回归;
对于无监督学习,该参数没有值。
axes : 3轴的数组,可选(默认=无)
用于绘制曲线的轴。
ylim : 元组,结构为(ymin,ymax),可选
定义绘制的最小和最大y值。
cv : 整数型, 交叉验证生成器或一个可迭代对象,可选
确定交叉验证拆分策略。
可能的输入是:
- 无(None),使用默认的5折交叉验证,
- 整数,用于指定折数。
- 交叉验证分割器,详见下文
- 可迭代的数据(训练,测试)拆分成的索引数组
对于整数或/None输入, 如果y是二分类或多分类,则使用StratifiedKFold作为交叉验证分割器。如果估算器不是分类类型或标签y不是二分类uo多分类,则使用KFold作为交叉验证分割器。
引用:有关可以在此处使用的交叉验证器的各种信息,请参见用户指南<cross_validation>
n_jobs : 整数或None, 可选(默认是None)
要并行运行的作业数。
除非在obj:`joblib.parallel_backend`上下文中,否则“ None``表示1。-1表示使用所有处理器。有关更多详细信息,请参见术语<n_jobs>`。
train_sizes : 类数组, 结构为 (n_ticks,), 浮点数或整数
训练示例的相对或绝对数量,将用于生成学习曲线。如果数据类型为浮点数,则将其视为训练集最大大小的一部分(由所选验证方法确定),即,它必须在(0,1]之内。否则,则将其解释为训练集的绝对大小。
请注意,为了进行分类,样本数量通常必须足够大,以包含每个类别中的至少一个样本。(默认值:np.linspace(0.1, 1.0, 5))
"""
if axes is None:
_, axes = plt.subplots(1, 3, figsize=(20, 5))
axes[0].set_title(title)
if ylim is not None:
axes[0].set_ylim(*ylim)
axes[0].set_xlabel("Training examples")
axes[0].set_ylabel("Score")
train_sizes, train_scores, test_scores, fit_times, _ = \
learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs,
train_sizes=train_sizes,
return_times=True)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
fit_times_mean = np.mean(fit_times, axis=1)
fit_times_std = np.std(fit_times, axis=1)
# 绘制学习曲线
axes[0].grid()
axes[0].fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
axes[0].fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1,
color="g")
axes[0].plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
axes[0].plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
axes[0].legend(loc="best")
# Plot n_samples vs fit_times
axes[1].grid()
axes[1].plot(train_sizes, fit_times_mean, 'o-')
axes[1].fill_between(train_sizes, fit_times_mean - fit_times_std,
fit_times_mean + fit_times_std, alpha=0.1)
axes[1].set_xlabel("Training examples")
axes[1].set_ylabel("fit_times")
axes[1].set_title("Scalability of the model")
# 绘制拟合时间与得分
axes[2].grid()
axes[2].plot(fit_times_mean, test_scores_mean, 'o-')
axes[2].fill_between(fit_times_mean, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1)
axes[2].set_xlabel("fit_times")
axes[2].set_ylabel("Score")
axes[2].set_title("Performance of the model")
return plt
fig, axes = plt.subplots(3, 2, figsize=(10, 15))
X, y = load_digits(return_X_y=True)
title = "Learning Curves (Naive Bayes)"
# 进行100次迭代交叉验证,以获得更平滑的平均测试和训练成绩曲线,每次将20%的数据随机选择为验证集。
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, axes=axes[:, 0], ylim=(0.7, 1.01),
cv=cv, n_jobs=4)
title = r"Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC的训练代价比较昂贵,因此我们进行的CV迭代次数较少:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, axes=axes[:, 1], ylim=(0.7, 1.01),
cv=cv, n_jobs=4)
plt.show()
脚本的总运行时间:(0分钟 4.601秒)




