高斯过程分类的概率预测¶
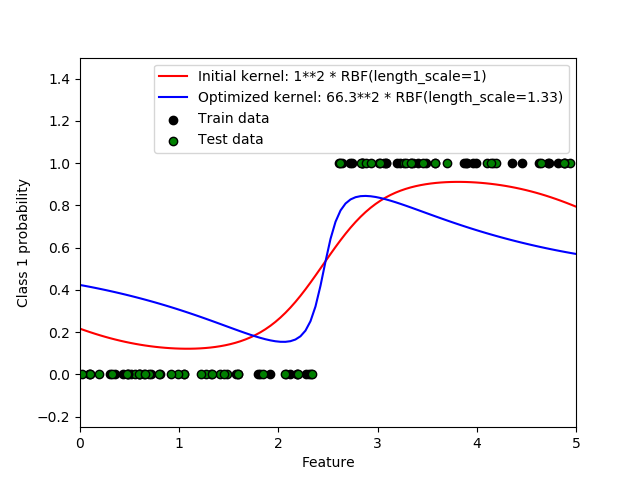
这个例子说明了在不同的超参数选择下,RBF核的GPC的预测概率。第一个图显示了具有任意选择的超参数和对应于最大对数边际似然(LML)的超参数的GPC的预测概率。
虽然通过优化LML选择的超参数具有相当大的LML,但根据测试数据的日志丢失情况,它们的性能略差一些。图中显示,这是因为它们在类边界上出现了类概率的急剧变化(这是好的),但是预测的概率接近于离类边界近0.5(这是不好的),这种不良影响是由GPC内部使用的Laplace近似引起的。
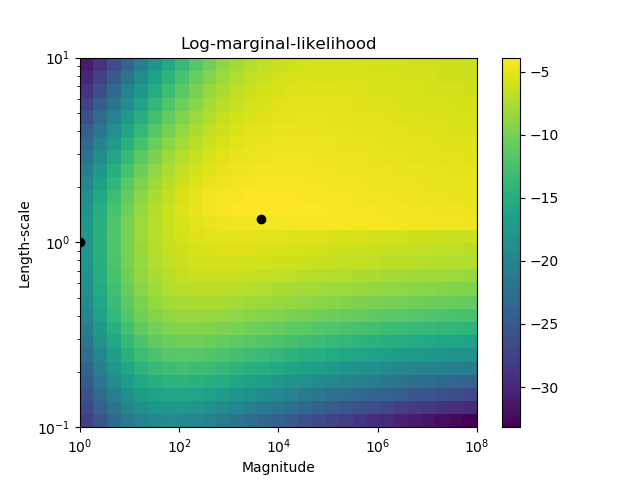
第二个图显示了内核的超参数的不同选择的对数边际似然,突出显示了在第一个图形中使用黑点的两个超参数选择。
Log Marginal Likelihood (initial): -17.598
Log Marginal Likelihood (optimized): -3.875
Accuracy: 1.000 (initial) 1.000 (optimized)
Log-loss: 0.214 (initial) 0.319 (optimized)
print(__doc__)
# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn.metrics import accuracy_score, log_loss
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
# Generate data
train_size = 50
rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 100)[:, np.newaxis]
y = np.array(X[:, 0] > 2.5, dtype=int)
# Specify Gaussian Processes with fixed and optimized hyperparameters
gp_fix = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0),
optimizer=None)
gp_fix.fit(X[:train_size], y[:train_size])
gp_opt = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0))
gp_opt.fit(X[:train_size], y[:train_size])
print("Log Marginal Likelihood (initial): %.3f"
% gp_fix.log_marginal_likelihood(gp_fix.kernel_.theta))
print("Log Marginal Likelihood (optimized): %.3f"
% gp_opt.log_marginal_likelihood(gp_opt.kernel_.theta))
print("Accuracy: %.3f (initial) %.3f (optimized)"
% (accuracy_score(y[:train_size], gp_fix.predict(X[:train_size])),
accuracy_score(y[:train_size], gp_opt.predict(X[:train_size]))))
print("Log-loss: %.3f (initial) %.3f (optimized)"
% (log_loss(y[:train_size], gp_fix.predict_proba(X[:train_size])[:, 1]),
log_loss(y[:train_size], gp_opt.predict_proba(X[:train_size])[:, 1])))
# Plot posteriors
plt.figure()
plt.scatter(X[:train_size, 0], y[:train_size], c='k', label="Train data",
edgecolors=(0, 0, 0))
plt.scatter(X[train_size:, 0], y[train_size:], c='g', label="Test data",
edgecolors=(0, 0, 0))
X_ = np.linspace(0, 5, 100)
plt.plot(X_, gp_fix.predict_proba(X_[:, np.newaxis])[:, 1], 'r',
label="Initial kernel: %s" % gp_fix.kernel_)
plt.plot(X_, gp_opt.predict_proba(X_[:, np.newaxis])[:, 1], 'b',
label="Optimized kernel: %s" % gp_opt.kernel_)
plt.xlabel("Feature")
plt.ylabel("Class 1 probability")
plt.xlim(0, 5)
plt.ylim(-0.25, 1.5)
plt.legend(loc="best")
# Plot LML landscape
plt.figure()
theta0 = np.logspace(0, 8, 30)
theta1 = np.logspace(-1, 1, 29)
Theta0, Theta1 = np.meshgrid(theta0, theta1)
LML = [[gp_opt.log_marginal_likelihood(np.log([Theta0[i, j], Theta1[i, j]]))
for i in range(Theta0.shape[0])] for j in range(Theta0.shape[1])]
LML = np.array(LML).T
plt.plot(np.exp(gp_fix.kernel_.theta)[0], np.exp(gp_fix.kernel_.theta)[1],
'ko', zorder=10)
plt.plot(np.exp(gp_opt.kernel_.theta)[0], np.exp(gp_opt.kernel_.theta)[1],
'ko', zorder=10)
plt.pcolor(Theta0, Theta1, LML)
plt.xscale("log")
plt.yscale("log")
plt.colorbar()
plt.xlabel("Magnitude")
plt.ylabel("Length-scale")
plt.title("Log-marginal-likelihood")
plt.show()
脚本的总运行时间:(0分3.016秒)




