真实数据集上的孤立点检测¶
此示例说明了对实际数据集进行稳健协方差估计的必要性。它对孤立点检测和更好地理解数据结构都是有用的。
我们从波士顿住房数据集中选择了两组两个变量,以说明使用几个孤立点检测工具可以进行什么样的分析。为了可视化的目的,我们使用了二维的例子,但是我们应该意识到,在高维中,事情并不像我们将要指出的那样简单。
在下面的两个例子中,主要的结果是经验协方差估计作为一种非稳健的估计,受观测的非均匀结构的影响很大。虽然稳健协方差估计能够集中于数据分布的主要模式,但它坚持了数据应该是高斯分布的假设,得到了一些对数据结构的有偏估计,但在一定程度上也是准确的。单类支持向量机不假设任何参数形式的数据分布,因此可以更好地模拟数据的复杂形状。
第一个例子
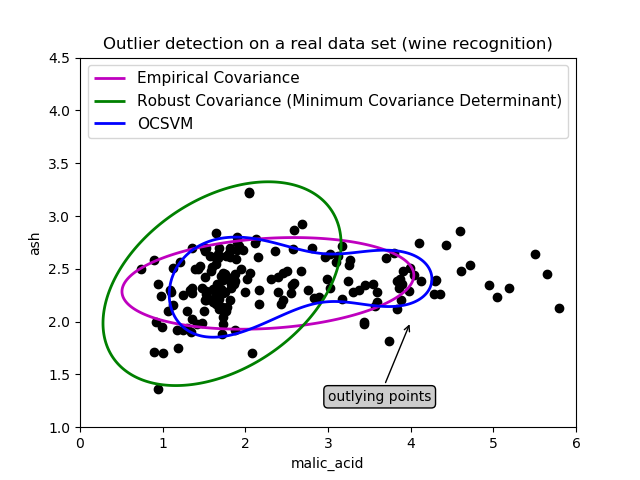
第一个例子说明了当存在离群点时,最小协方差行列式稳健估计器如何帮助集中于相关的聚类。这里,经验协方差估计被主聚类以外的点所扭曲。当然,一些筛选工具会指出存在两个聚类(支持向量机、高斯混合模型、单变量孤立点检测、…)。但如果这是一个高维的例子,这些都不可能那么容易应用。
print(__doc__)
# Author: Virgile Fritsch <virgile.fritsch@inria.fr>
# License: BSD 3 clause
import numpy as np
from sklearn.covariance import EllipticEnvelope
from sklearn.svm import OneClassSVM
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn.datasets import load_wine
# Define "classifiers" to be used
classifiers = {
"Empirical Covariance": EllipticEnvelope(support_fraction=1.,
contamination=0.25),
"Robust Covariance (Minimum Covariance Determinant)":
EllipticEnvelope(contamination=0.25),
"OCSVM": OneClassSVM(nu=0.25, gamma=0.35)}
colors = ['m', 'g', 'b']
legend1 = {}
legend2 = {}
# Get data
X1 = load_wine()['data'][:, [1, 2]] # two clusters
# Learn a frontier for outlier detection with several classifiers
xx1, yy1 = np.meshgrid(np.linspace(0, 6, 500), np.linspace(1, 4.5, 500))
for i, (clf_name, clf) in enumerate(classifiers.items()):
plt.figure(1)
clf.fit(X1)
Z1 = clf.decision_function(np.c_[xx1.ravel(), yy1.ravel()])
Z1 = Z1.reshape(xx1.shape)
legend1[clf_name] = plt.contour(
xx1, yy1, Z1, levels=[0], linewidths=2, colors=colors[i])
legend1_values_list = list(legend1.values())
legend1_keys_list = list(legend1.keys())
# Plot the results (= shape of the data points cloud)
plt.figure(1) # two clusters
plt.title("Outlier detection on a real data set (wine recognition)")
plt.scatter(X1[:, 0], X1[:, 1], color='black')
bbox_args = dict(boxstyle="round", fc="0.8")
arrow_args = dict(arrowstyle="->")
plt.annotate("outlying points", xy=(4, 2),
xycoords="data", textcoords="data",
xytext=(3, 1.25), bbox=bbox_args, arrowprops=arrow_args)
plt.xlim((xx1.min(), xx1.max()))
plt.ylim((yy1.min(), yy1.max()))
plt.legend((legend1_values_list[0].collections[0],
legend1_values_list[1].collections[0],
legend1_values_list[2].collections[0]),
(legend1_keys_list[0], legend1_keys_list[1], legend1_keys_list[2]),
loc="upper center",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.ylabel("ash")
plt.xlabel("malic_acid")
plt.show()
第二个例子
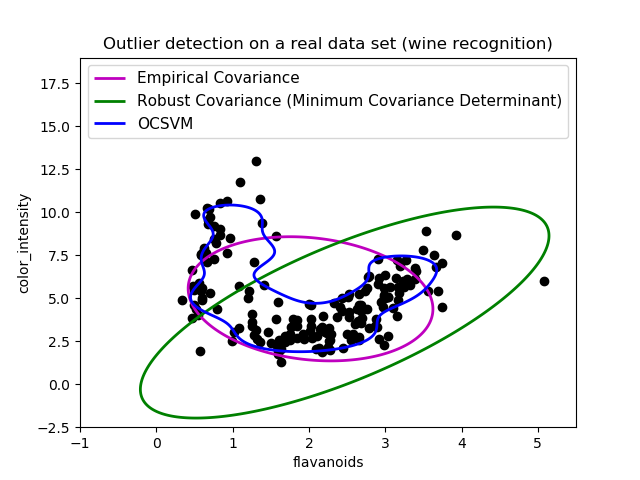
第二个例子显示了协方差的最小协方差行列式稳健估计器能够集中于数据分布的主要模式:局部似乎被很好地估计,尽管由于香蕉形状的分布,协方差很难估计。总之,我们可以去掉一些外围的观测点。一类支持向量机能够捕捉到真实的数据结构,但其难点在于调整其核带宽参数,从而使数据点矩阵的形状与数据过度拟合的风险得到很好的控制。
# Get data
X2 = load_wine()['data'][:, [6, 9]] # "banana"-shaped
# Learn a frontier for outlier detection with several classifiers
xx2, yy2 = np.meshgrid(np.linspace(-1, 5.5, 500), np.linspace(-2.5, 19, 500))
for i, (clf_name, clf) in enumerate(classifiers.items()):
plt.figure(2)
clf.fit(X2)
Z2 = clf.decision_function(np.c_[xx2.ravel(), yy2.ravel()])
Z2 = Z2.reshape(xx2.shape)
legend2[clf_name] = plt.contour(
xx2, yy2, Z2, levels=[0], linewidths=2, colors=colors[i])
legend2_values_list = list(legend2.values())
legend2_keys_list = list(legend2.keys())
# Plot the results (= shape of the data points cloud)
plt.figure(2) # "banana" shape
plt.title("Outlier detection on a real data set (wine recognition)")
plt.scatter(X2[:, 0], X2[:, 1], color='black')
plt.xlim((xx2.min(), xx2.max()))
plt.ylim((yy2.min(), yy2.max()))
plt.legend((legend2_values_list[0].collections[0],
legend2_values_list[1].collections[0],
legend2_values_list[2].collections[0]),
(legend2_keys_list[0], legend2_keys_list[1], legend2_keys_list[2]),
loc="upper center",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.ylabel("color_intensity")
plt.xlabel("flavanoids")
plt.show()
 脚本的总运行时间:(0分1.259秒)
脚本的总运行时间:(0分1.259秒)
Download Python source code: plot_outlier_detection_wine.py
Download Jupyter notebook: plot_outlier_detection_wine.ipynb




