具有成本复杂度的后剪枝决策树¶

DecisionTreeClassifier 提供了一些参数，如 min_samples_leaf和max_depth，以防止树过拟合。成本复杂度剪枝提供了另一个控制树大小的选项。在 DecisionTreeClassifier中， 这种剪枝技术是通过成本复杂度参数ccp_alpha来参数化的。更大的ccp_alpha值增加被剪枝的节点数。这里我们只展示了 ccp_alpha对树的正则化的影响，以及如何根据验证分数来选择ccp_alpha。

有关剪枝的详细信息，请参见最小成本复杂度剪枝。

print(__doc__)
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.tree import DecisionTreeClassifier

叶子的总不存度 VS 被剪枝树的有效alphas

最小成本复杂度剪枝是递归地找到 “weakest link”的节点。 weakest link是一个通过有效的 alpha进行参数化的，其中最小的有效的alpha的节点首先被剪枝。

为了了解ccp_alpha的哪些值可能是合适的，scikit-learn提供了DecisionTreeClassifier.cost_complexity_pruning_path在修剪过程中每一步返回有效的alphas和相应的总叶子不存度。随着alpha的增加，更多的树被修剪，这增加了它的叶子的总不存度。

X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

在下面的图中，最大有效alpha值被删除，因为它是只有一个节点的很普通的树。

fig, ax = plt.subplots()
ax.plot(ccp_alphas[:-1], impurities[:-1], marker='o', drawstyle="steps-post")
ax.set_xlabel("effective alpha")
ax.set_ylabel("total impurity of leaves")
ax.set_title("Total Impurity vs effective alpha for training set")

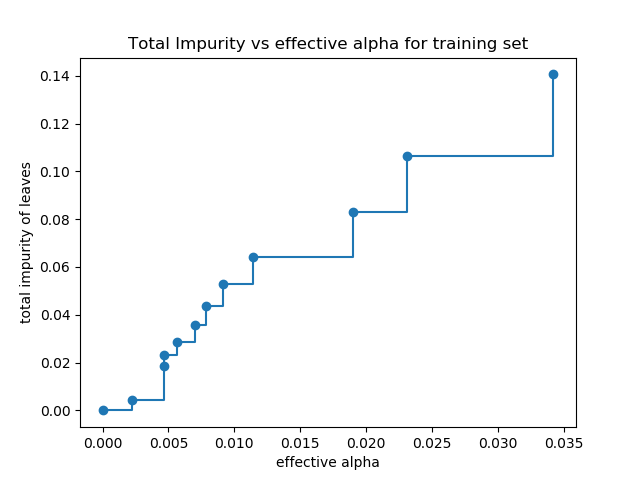
Text(0.5, 1.0, 'Total Impurity vs effective alpha for training set')

接下来，我们使用有效的alphas来训练决策树。 ccp_alphas中的最后一个值是修剪整棵树的alpha值，而树clfs[-1]只有一个节点。

clfs = []
for ccp_alpha in ccp_alphas:
    clf = DecisionTreeClassifier(random_state=0, ccp_alpha=ccp_alpha)
    clf.fit(X_train, y_train)
    clfs.append(clf)
print("Number of nodes in the last tree is: {} with ccp_alpha: {}".format(
      clfs[-1].tree_.node_count, ccp_alphas[-1]))

Number of nodes in the last tree is: 1 with ccp_alpha: 0.3272984419327777

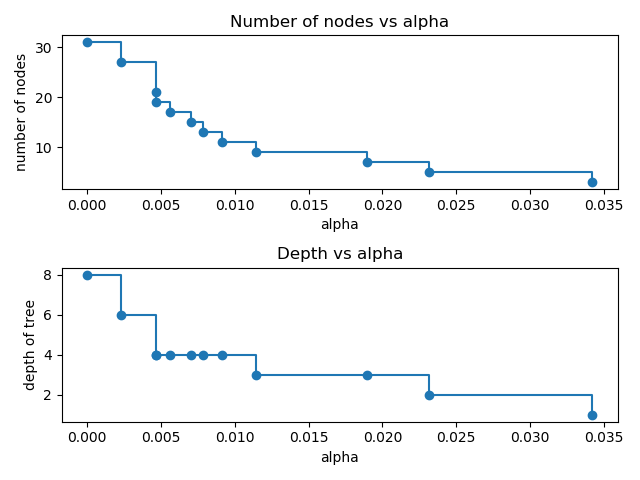
对于本例的其余部分，我们移除 clfs 和ccp_alphas中的最后一个元素，因为它是只有一个节点的很普通的树。在这里，我们证明了节点数和树的深度随着 alpha 的增加而减少。

clfs = clfs[:-1]
ccp_alphas = ccp_alphas[:-1]

node_counts = [clf.tree_.node_count for clf in clfs]
depth = [clf.tree_.max_depth for clf in clfs]
fig, ax = plt.subplots(2, 1)
ax[0].plot(ccp_alphas, node_counts, marker='o', drawstyle="steps-post")
ax[0].set_xlabel("alpha")
ax[0].set_ylabel("number of nodes")
ax[0].set_title("Number of nodes vs alpha")
ax[1].plot(ccp_alphas, depth, marker='o', drawstyle="steps-post")
ax[1].set_xlabel("alpha")
ax[1].set_ylabel("depth of tree")
ax[1].set_title("Depth vs alpha")
fig.tight_layout()

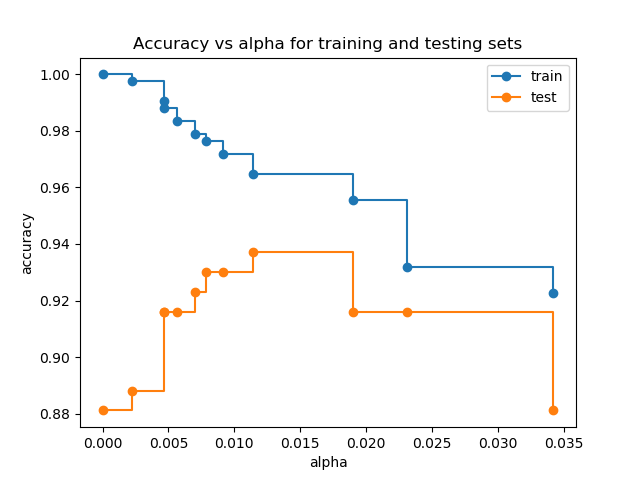
训练和测试集的准确率 vs alpha

当 ccp_alpha 设置为0, 并保留DecisionTreeClassifier的其他默认参数时, 树就过拟合了，使训练的准确率达到100%，测试的准确率达到88%。随着alpha的增加，更多的树被剪枝，从而创建了一个泛化更好的决策树。在本例中，设置 ccp_alpha=0.015可以最大限度地提高测试的准确率。

train_scores = [clf.score(X_train, y_train) for clf in clfs]
test_scores = [clf.score(X_test, y_test) for clf in clfs]

fig, ax = plt.subplots()
ax.set_xlabel("alpha")
ax.set_ylabel("accuracy")
ax.set_title("Accuracy vs alpha for training and testing sets")
ax.plot(ccp_alphas, train_scores, marker='o', label="train",
        drawstyle="steps-post")
ax.plot(ccp_alphas, test_scores, marker='o', label="test",
        drawstyle="steps-post")
ax.legend()
plt.show()

脚本的总运行时间：(0分0.427秒)

Download Python source code: plot_cost_complexity_pruning.py

Download Jupyter notebook:plot_cost_complexity_pruning.ipynb