贝叶斯岭回归¶
在合成数据集上计算贝叶斯岭回归。
有关回归的更多信息,请参见贝叶斯岭回归。
与普通最小二乘估计相比,系数权值略有移向零,从而使其稳定。
由于权值的先验是高斯先验,估计权值的直方图是高斯的。
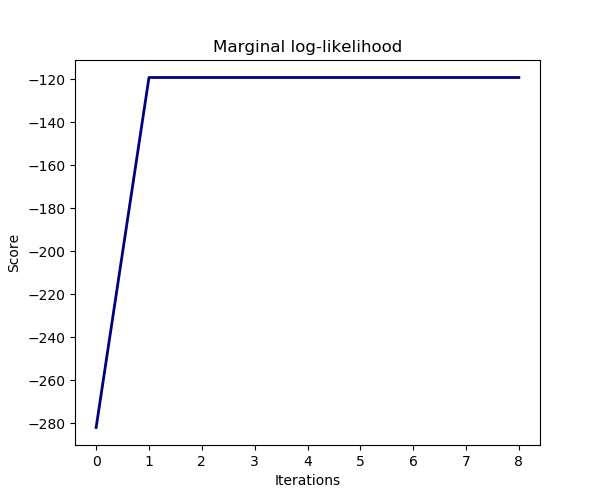
模型的估计是通过迭代最大化观测的边际对数似然来实现的。
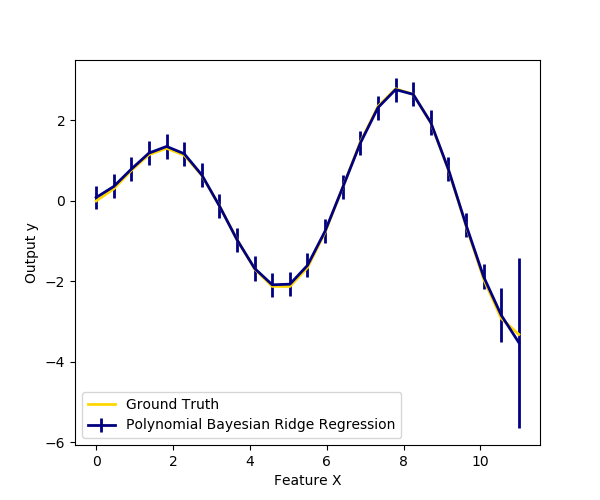
我们还用多项式特征扩展法绘制了一维回归的贝叶斯岭回归的预测和不确定性图。请注意,在右边的图中不确定性开始上升这是因为这些测试样本超出了训练样本的范围。


print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.linear_model import BayesianRidge, LinearRegression
# #############################################################################
# Generating simulated data with Gaussian weights
np.random.seed(0)
n_samples, n_features = 100, 100
X = np.random.randn(n_samples, n_features) # Create Gaussian data
# Create weights with a precision lambda_ of 4.
lambda_ = 4.
w = np.zeros(n_features)
# Only keep 10 weights of interest
relevant_features = np.random.randint(0, n_features, 10)
for i in relevant_features:
w[i] = stats.norm.rvs(loc=0, scale=1. / np.sqrt(lambda_))
# Create noise with a precision alpha of 50.
alpha_ = 50.
noise = stats.norm.rvs(loc=0, scale=1. / np.sqrt(alpha_), size=n_samples)
# Create the target
y = np.dot(X, w) + noise
# #############################################################################
# Fit the Bayesian Ridge Regression and an OLS for comparison
clf = BayesianRidge(compute_score=True)
clf.fit(X, y)
ols = LinearRegression()
ols.fit(X, y)
# #############################################################################
# Plot true weights, estimated weights, histogram of the weights, and
# predictions with standard deviations
lw = 2
plt.figure(figsize=(6, 5))
plt.title("Weights of the model")
plt.plot(clf.coef_, color='lightgreen', linewidth=lw,
label="Bayesian Ridge estimate")
plt.plot(w, color='gold', linewidth=lw, label="Ground truth")
plt.plot(ols.coef_, color='navy', linestyle='--', label="OLS estimate")
plt.xlabel("Features")
plt.ylabel("Values of the weights")
plt.legend(loc="best", prop=dict(size=12))
plt.figure(figsize=(6, 5))
plt.title("Histogram of the weights")
plt.hist(clf.coef_, bins=n_features, color='gold', log=True,
edgecolor='black')
plt.scatter(clf.coef_[relevant_features], np.full(len(relevant_features), 5.),
color='navy', label="Relevant features")
plt.ylabel("Features")
plt.xlabel("Values of the weights")
plt.legend(loc="upper left")
plt.figure(figsize=(6, 5))
plt.title("Marginal log-likelihood")
plt.plot(clf.scores_, color='navy', linewidth=lw)
plt.ylabel("Score")
plt.xlabel("Iterations")
# Plotting some predictions for polynomial regression
def f(x, noise_amount):
y = np.sqrt(x) * np.sin(x)
noise = np.random.normal(0, 1, len(x))
return y + noise_amount * noise
degree = 10
X = np.linspace(0, 10, 100)
y = f(X, noise_amount=0.1)
clf_poly = BayesianRidge()
clf_poly.fit(np.vander(X, degree), y)
X_plot = np.linspace(0, 11, 25)
y_plot = f(X_plot, noise_amount=0)
y_mean, y_std = clf_poly.predict(np.vander(X_plot, degree), return_std=True)
plt.figure(figsize=(6, 5))
plt.errorbar(X_plot, y_mean, y_std, color='navy',
label="Polynomial Bayesian Ridge Regression", linewidth=lw)
plt.plot(X_plot, y_plot, color='gold', linewidth=lw,
label="Ground Truth")
plt.ylabel("Output y")
plt.xlabel("Feature X")
plt.legend(loc="lower left")
plt.show()
脚本的总运行时间:(0分0.500秒)




