绘制正则化函数的岭系数图¶
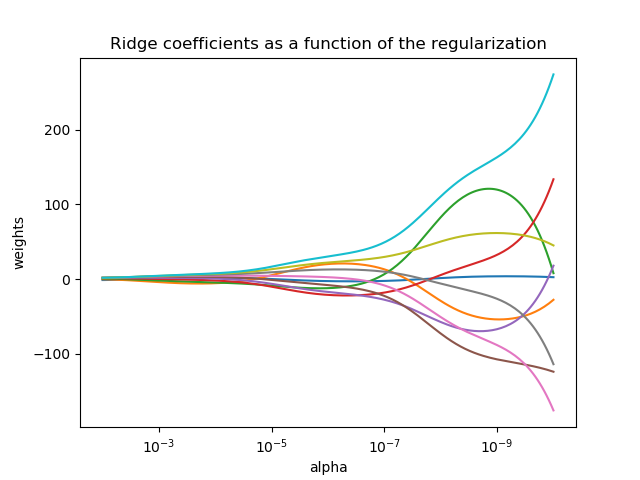
该图显示了估计器系数的共线性的影响。
岭回归是在这个例子中使用的估计器。每种颜色都表示系数向量的不同特征,这将显示为正则化参数的函数。
此示例还显示了将岭回归应用于高度病态矩阵的有效性。对于这样的矩阵,目标变量的微小变化会导致计算权重的巨大差异。在这种情况下,设置一定的正则化(Alpha)以减少这种变化(噪声)是有用的。
当alpha很大时,正则化效应控制平方损失函数,系数趋于零。在路径的末尾,当alpha趋于零,解趋于普通的最小二乘时,系数会出现很大的振荡。在实践中,有必要对alpha进行调优,以便在两者之间保持平衡。
# Author: Fabian Pedregosa -- <fabian.pedregosa@inria.fr>
# License: BSD 3 clause
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
# #############################################################################
# Compute paths
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
coefs = []
for a in alphas:
ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
ridge.fit(X, y)
coefs.append(ridge.coef_)
# #############################################################################
# Display results
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()
脚本的总运行时间:(0分0.174秒)




