toy数据集上不同层次链接方法的比较¶
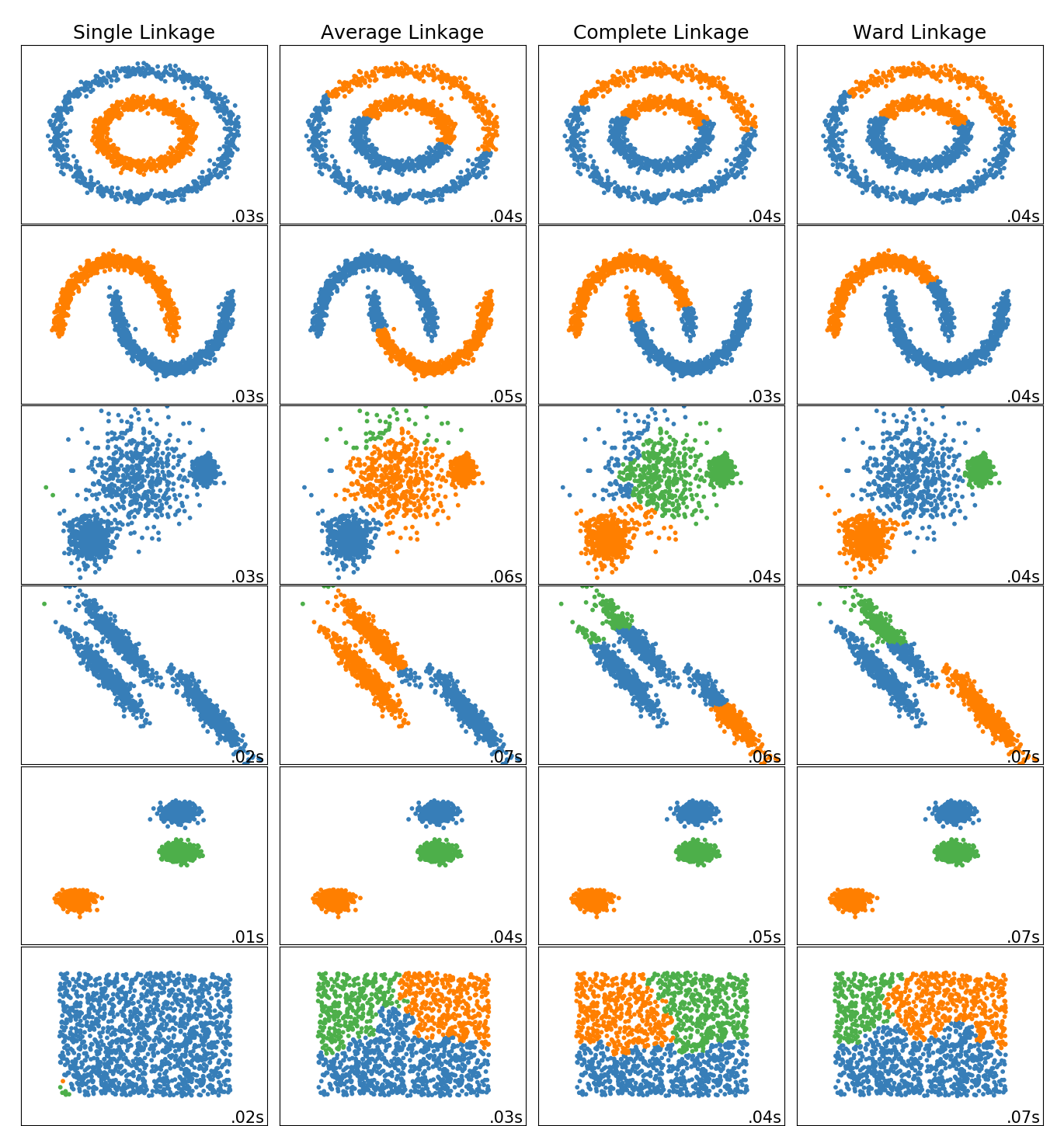
这个例子展示了不同的链接方法在数据集上的分层聚类的特点,这些方法是“interesting”,但仍然是2D的。
主要观察结果如下:
单链接速度快,可以很好地处理非球形数据,但在存在噪声的情况下性能较差。 平均和完全链接表现良好, 干净分离球状簇,但有混合的结果。 Ward是处理含噪数据的最有效方法。
虽然这些例子给出了一些关于算法的直觉,但这种直觉可能不适用于非常高维的数据。
print(__doc__)
import time
import warnings
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
np.random.seed(0)
生成数据集。我们选择的大小足够大,足以看到算法的可伸缩性,但不要太大了,以避免太长的运行时间。
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5,
noise=.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None
# Anisotropicly distributed data
random_state = 170
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)
# blobs with varied variances
varied = datasets.make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
执行聚类和绘图
# Set up cluster parameters
plt.figure(figsize=(9 * 1.3 + 2, 14.5))
plt.subplots_adjust(left=.02, right=.98, bottom=.001, top=.96, wspace=.05,
hspace=.01)
plot_num = 1
default_base = {'n_neighbors': 10,
'n_clusters': 3}
datasets = [
(noisy_circles, {'n_clusters': 2}),
(noisy_moons, {'n_clusters': 2}),
(varied, {'n_neighbors': 2}),
(aniso, {'n_neighbors': 2}),
(blobs, {}),
(no_structure, {})]
for i_dataset, (dataset, algo_params) in enumerate(datasets):
# update parameters with dataset-specific values
params = default_base.copy()
params.update(algo_params)
X, y = dataset
# normalize dataset for easier parameter selection
X = StandardScaler().fit_transform(X)
# ============
# Create cluster objects
# ============
ward = cluster.AgglomerativeClustering(
n_clusters=params['n_clusters'], linkage='ward')
complete = cluster.AgglomerativeClustering(
n_clusters=params['n_clusters'], linkage='complete')
average = cluster.AgglomerativeClustering(
n_clusters=params['n_clusters'], linkage='average')
single = cluster.AgglomerativeClustering(
n_clusters=params['n_clusters'], linkage='single')
clustering_algorithms = (
('Single Linkage', single),
('Average Linkage', average),
('Complete Linkage', complete),
('Ward Linkage', ward),
)
for name, algorithm in clustering_algorithms:
t0 = time.time()
# catch warnings related to kneighbors_graph
with warnings.catch_warnings():
warnings.filterwarnings(
"ignore",
message="the number of connected components of the " +
"connectivity matrix is [0-9]{1,2}" +
" > 1. Completing it to avoid stopping the tree early.",
category=UserWarning)
algorithm.fit(X)
t1 = time.time()
if hasattr(algorithm, 'labels_'):
y_pred = algorithm.labels_.astype(np.int)
else:
y_pred = algorithm.predict(X)
plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
if i_dataset == 0:
plt.title(name, size=18)
colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a',
'#f781bf', '#a65628', '#984ea3',
'#999999', '#e41a1c', '#dede00']),
int(max(y_pred) + 1))))
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.xticks(())
plt.yticks(())
plt.text(.99, .01, ('%.2fs' % (t1 - t0)).lstrip('0'),
transform=plt.gca().transAxes, size=15,
horizontalalignment='right')
plot_num += 1
plt.show()
脚本的总运行时间:(0分2.671秒)




