物种分布的核密度估计¶
在这里展示的是一个基于最近邻查询的案例,该案例使用基于Haversine距离度量(即,经度/纬度上的点的距离)构建的球树(Ball Tree),对地理空间数据进行最近邻查询(尤其是内核密度估计)。数据集由Phillips等人在2006年发表的论文中提供。 如果可以,该案例将使用basemap库绘制南美的海岸线和国家边界。
本案例不对数据进行任何学习(有关基于此数据集中属性的分类示例,请参阅物种分布建模)。 它仅显示了地理空间坐标中观察到的数据点的核密度估计。
这两种生物是:
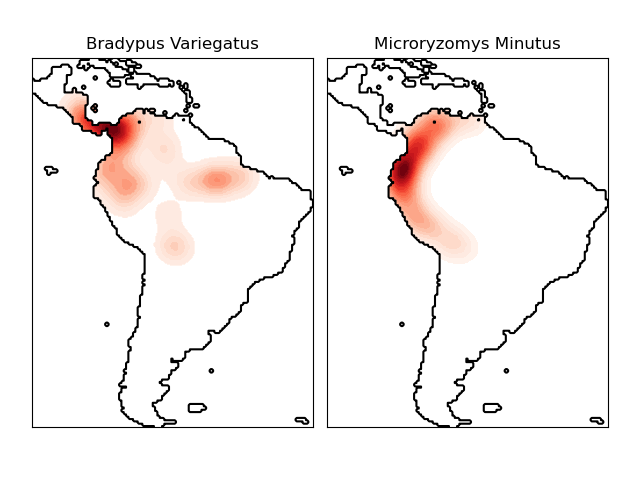
“Bradypus variegatus”,一种棕喉树懒
“ Microryzomys minutus”,也称为森林小稻鼠,一种生活在秘鲁,哥伦比亚,厄瓜多尔,秘鲁和委内瑞拉的啮齿动物。
引用
“Maximum entropy modeling of species geographic distributions” S. J. Phillips, R. P. Anderson, R. E. Schapire - Ecological Modelling, 190:231-259, 2006.
输出:
- computing KDE in spherical coordinates
- plot coastlines from coverage
- computing KDE in spherical coordinates
- plot coastlines from coverage
输入:
# 作者: Jake Vanderplas <jakevdp@cs.washington.edu>
#
# 执照: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_species_distributions
from sklearn.neighbors import KernelDensity
# 如果basemap库可用,我们可以使用它:
# 否则,我们之后在看看如何处理
try:
from mpl_toolkits.basemap import Basemap
basemap = True
except ImportError:
basemap = False
def construct_grids(batch):
"""从批处理对象构造地图网格
参数
----------
batch : 批处理对象
功能 :func:`fetch_species_distributions`返回的对象
输出
-------
(xgrid, ygrid) : 1维数组
对应于batch.coverages中的值的网格
"""
# 角单元的x,y坐标
xmin = batch.x_left_lower_corner + batch.grid_size
xmax = xmin + (batch.Nx * batch.grid_size)
ymin = batch.y_left_lower_corner + batch.grid_size
ymax = ymin + (batch.Ny * batch.grid_size)
# 网格单元的x坐标
xgrid = np.arange(xmin, xmax, batch.grid_size)
# 网格单元的y坐标
ygrid = np.arange(ymin, ymax, batch.grid_size)
return (xgrid, ygrid)
# 获取物种ID和位置的矩阵/数组
data = fetch_species_distributions()
species_names = ['Bradypus Variegatus', 'Microryzomys Minutus']
Xtrain = np.vstack([data['train']['dd lat'],
data['train']['dd long']]).T
ytrain = np.array([d.decode('ascii').startswith('micro')
for d in data['train']['species']], dtype='int')
Xtrain *= np.pi / 180. # Convert lat/long to radians
# 设置等高线图的数据网格
xgrid, ygrid = construct_grids(data)
X, Y = np.meshgrid(xgrid[::5], ygrid[::5][::-1])
land_reference = data.coverages[6][::5, ::5]
land_mask = (land_reference > -9999).ravel()
xy = np.vstack([Y.ravel(), X.ravel()]).T
xy = xy[land_mask]
xy *= np.pi / 180.
# 绘制南美洲的地图,每种物种的分布
fig = plt.figure()
fig.subplots_adjust(left=0.05, right=0.95, wspace=0.05)
for i in range(2):
plt.subplot(1, 2, i + 1)
# 构造分布的核密度估计
print(" - computing KDE in spherical coordinates")
kde = KernelDensity(bandwidth=0.04, metric='haversine',
kernel='gaussian', algorithm='ball_tree')
kde.fit(Xtrain[ytrain == i])
# 仅在陆地上评估:-9999表示海洋
Z = np.full(land_mask.shape[0], -9999, dtype='int')
Z[land_mask] = np.exp(kde.score_samples(xy))
Z = Z.reshape(X.shape)
# 绘制密度等高线
levels = np.linspace(0, Z.max(), 25)
plt.contourf(X, Y, Z, levels=levels, cmap=plt.cm.Reds)
if basemap:
print(" - plot coastlines using basemap")
m = Basemap(projection='cyl', llcrnrlat=Y.min(),
urcrnrlat=Y.max(), llcrnrlon=X.min(),
urcrnrlon=X.max(), resolution='c')
m.drawcoastlines()
m.drawcountries()
else:
print(" - plot coastlines from coverage")
plt.contour(X, Y, land_reference,
levels=[-9998], colors="k",
linestyles="solid")
plt.xticks([])
plt.yticks([])
plt.title(species_names[i])
plt.show()
脚本的总运行时间:(0分钟7.247秒)




