F检验与互换信息法的比较¶
此示例说明了单变量F检验统计量与互换信息法之间的差异。
我们考虑三个特征x_1,x_2,x_3均匀分布在[0,1]上,目标变量依赖于它们:
y = x_1 + sin(6 * pi * x_2) + 0.1 * N(0, 1), 也就是说,第三个特性是完全不相关的。
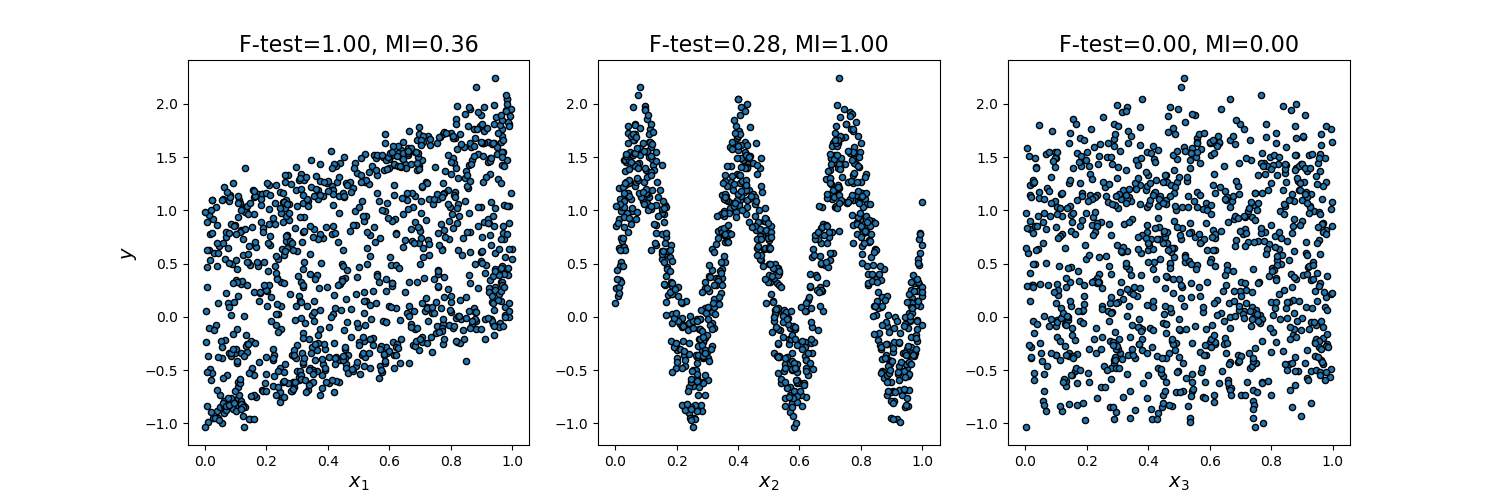
下面代码绘制了y对单个x_i的依懒性, 并且归一化了单变量F检验统计和互换信息法的值。
因为F检验只能捕捉线性关系, 所以它将x_1评为最具判断力的特征。另一方面,互换信息法可以捕捉变量之间的任何类型的关系,所以它将x_2评为最具判断力的特性,这可能更符合我们对这个例子的直觉。这两种方法都正确地将x_3标记为无关。
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_selection import f_regression, mutual_info_regression
np.random.seed(0)
X = np.random.rand(1000, 3)
y = X[:, 0] + np.sin(6 * np.pi * X[:, 1]) + 0.1 * np.random.randn(1000)
f_test, _ = f_regression(X, y)
f_test /= np.max(f_test)
mi = mutual_info_regression(X, y)
mi /= np.max(mi)
plt.figure(figsize=(15, 5))
for i in range(3):
plt.subplot(1, 3, i + 1)
plt.scatter(X[:, i], y, edgecolor='black', s=20)
plt.xlabel("$x_{}$".format(i + 1), fontsize=14)
if i == 0:
plt.ylabel("$y$", fontsize=14)
plt.title("F-test={:.2f}, MI={:.2f}".format(f_test[i], mi[i]),
fontsize=16)
plt.show()
脚本的总运行时间:(0分0.292秒)




