泊松回归与非正常损失¶
此示例说明了在法国电机第三方责任索赔数据集[1]中使用对数线性泊松回归的方法，并将其与普通最小二乘误差的线性模型和具有泊松损失(和日志链接)的非线性GBRT模型进行了比较。
一些定义：
保单是保险公司和个人之间的合同：投保人，也就是在这种情况下的车辆司机。 索赔是指投保人向保险公司提出的赔偿保险损失的请求。 风险敞口是以年数为单位的某一特定保单的保险承保期限。 索赔频率是索赔的数量除以风险，通常以每年的索赔件数来衡量。
在此数据集中，每个示例对应于保险单。可用的特征包括驾驶年龄，车辆年龄，车辆动力等。
我们的目标是根据历史数据预测新投保人在车祸后索赔的预期频率。
1 A. Noll, R. Salzmann and M.V. Wuthrich, Case Study: French Motor Third-Party Liability Claims (November 8, 2018). doi:10.2139/ssrn.3164764
print(__doc__)
# Authors: Christian Lorentzen <lorentzen.ch@gmail.com>
# Roman Yurchak <rth.yurchak@gmail.com>
# Olivier Grisel <olivier.grisel@ensta.org>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
法国汽车第三方责任索赔数据集
让我们从OpenML加载motor claim数据集：https://www.openml.org/d/41214
from sklearn.datasets import fetch_openml
df = fetch_openml(data_id=41214, as_frame=True).frame
df
/home/circleci/project/sklearn/datasets/_openml.py:754: UserWarning: Version 1 of dataset freMTPL2freq is inactive, meaning that issues have been found in the dataset. Try using a newer version from this URL: https://www.openml.org/data/v1/download/20649148/freMTPL2freq.arff
warn("Version {} of dataset {} is inactive, meaning that issues have "
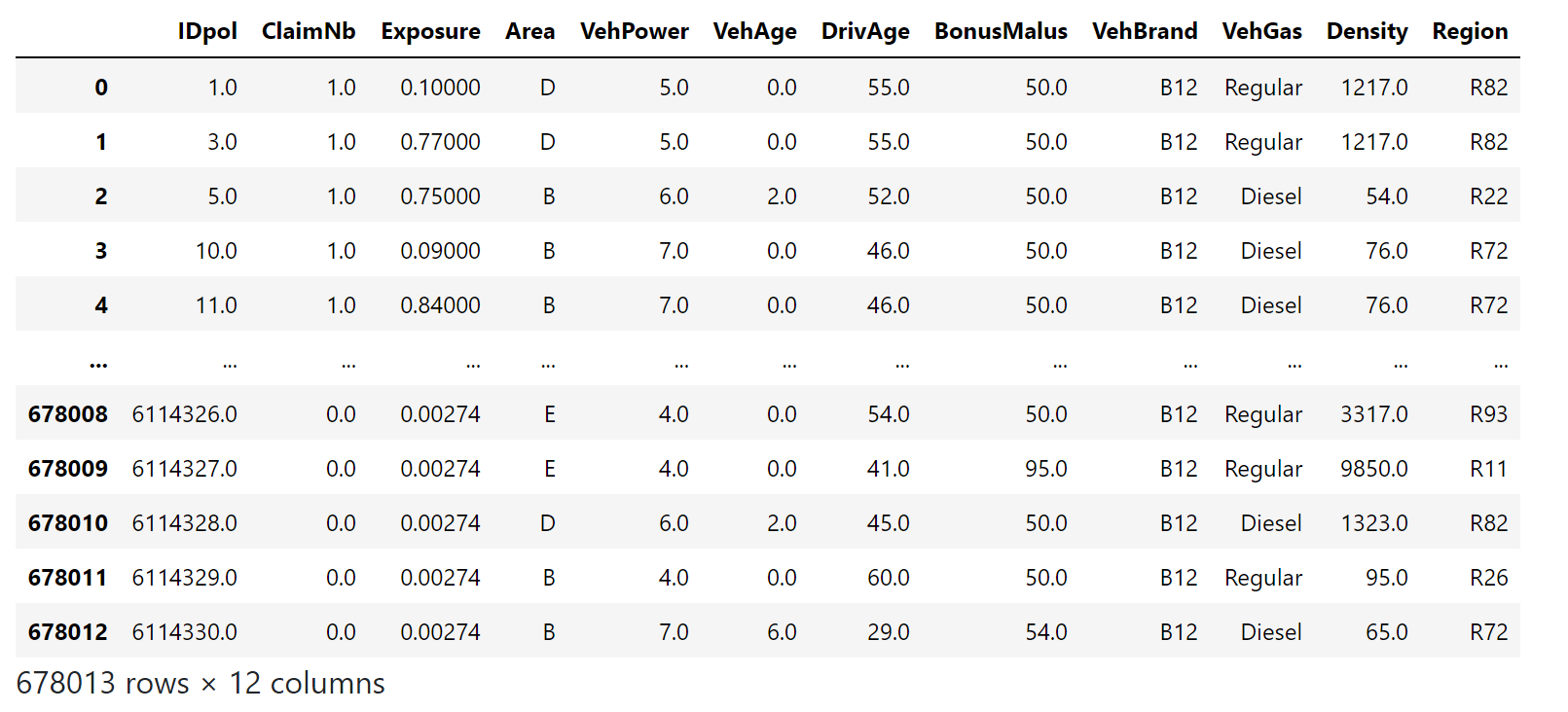索赔数量(ClaimNb)是一个正整数，可以建模为泊松分布。然后假定为在给定时间间隔内以恒定速率发生的离散事件的数量(Exposure,以年为单位)。
在这里，我们要通过一个(尺度)泊松分布来模拟频率 y = ClaimNb / Exposure 在X上的条件，并以 Exposure 作为sample_weight。
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
print("Average Frequency = {}"
.format(np.average(df["Frequency"], weights=df["Exposure"])))
print("Fraction of exposure with zero claims = {0:.1%}"
.format(df.loc[df["ClaimNb"] == 0, "Exposure"].sum() /
df["Exposure"].sum()))
fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(16, 4))
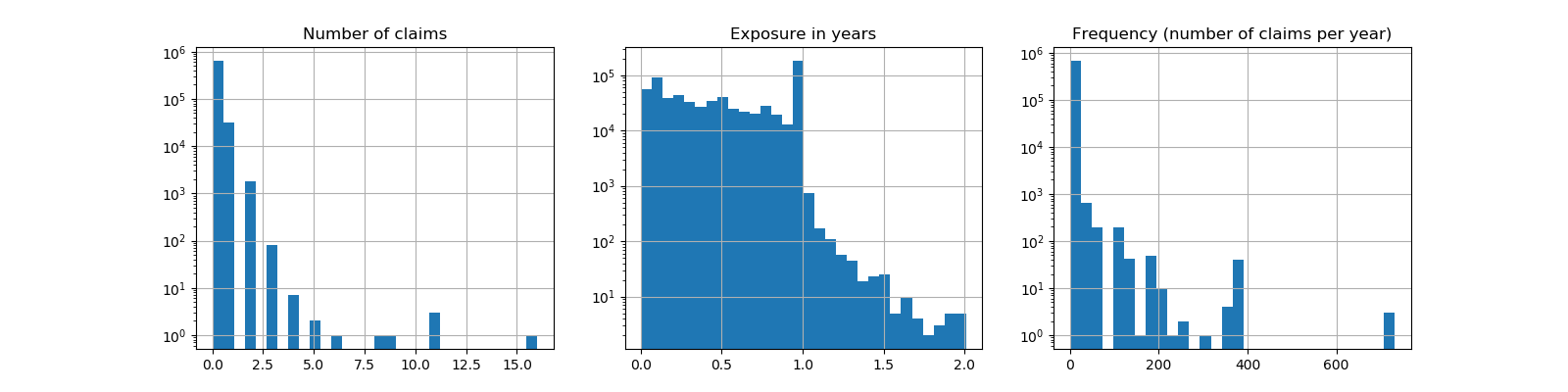
ax0.set_title("Number of claims")
_ = df["ClaimNb"].hist(bins=30, log=True, ax=ax0)
ax1.set_title("Exposure in years")
_ = df["Exposure"].hist(bins=30, log=True, ax=ax1)
ax2.set_title("Frequency (number of claims per year)")
_ = df["Frequency"].hist(bins=30, log=True, ax=ax2)
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
print("Average Frequency = {}"
.format(np.average(df["Frequency"], weights=df["Exposure"])))
print("Fraction of exposure with zero claims = {0:.1%}"
.format(df.loc[df["ClaimNb"] == 0, "Exposure"].sum() /
df["Exposure"].sum()))
fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(16, 4))
ax0.set_title("Number of claims")
_ = df["ClaimNb"].hist(bins=30, log=True, ax=ax0)
ax1.set_title("Exposure in years")
_ = df["Exposure"].hist(bins=30, log=True, ax=ax1)
ax2.set_title("Frequency (number of claims per year)")
_ = df["Frequency"].hist(bins=30, log=True, ax=ax2)
Average Frequency = 0.10070308464041304
Fraction of exposure with zero claims = 93.9%
其余的列可用于预测索赔事件的发生频率。这些列是非常异构的，具有不同比例的分类变量和数值变量的混合，可能分布非常不均匀。
因此，为了使线性模型与这些预测器相匹配，有必要执行以下标准特征转换：
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.compose import ColumnTransformer
log_scale_transformer = make_pipeline(
FunctionTransformer(np.log, validate=False),
StandardScaler()
)
linear_model_preprocessor = ColumnTransformer(
[
("passthrough_numeric", "passthrough",
["BonusMalus"]),
("binned_numeric", KBinsDiscretizer(n_bins=10),
["VehAge", "DrivAge"]),
("log_scaled_numeric", log_scale_transformer,
["Density"]),
("onehot_categorical", OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
],
remainder="drop",
)
恒定预测基线
值得注意的是，超过93%的投保人是没有索赔的。如果我们把这个问题转化为一个二分类任务，它显然是不平衡的，即使是一个简单的只预测均值的模型也能达到93%的精度。
为了评估使用的指标的相关性，我们将把一个“虚拟”估计器作为基线，它不断地预测训练样本的平均频率。
from sklearn.dummy import DummyRegressor
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
df_train, df_test = train_test_split(df, test_size=0.33, random_state=0)
dummy = Pipeline([
("preprocessor", linear_model_preprocessor),
("regressor", DummyRegressor(strategy='mean')),
]).fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
让我们用3种不同的回归度量来计算这个恒定预测基线的性能：
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_poisson_deviance
def score_estimator(estimator, df_test):
"""Score an estimator on the test set."""
y_pred = estimator.predict(df_test)
print("MSE: %.3f" %
mean_squared_error(df_test["Frequency"], y_pred,
sample_weight=df_test["Exposure"]))
print("MAE: %.3f" %
mean_absolute_error(df_test["Frequency"], y_pred,
sample_weight=df_test["Exposure"]))
# Ignore non-positive predictions, as they are invalid for
# the Poisson deviance.
mask = y_pred > 0
if (~mask).any():
n_masked, n_samples = (~mask).sum(), mask.shape[0]
print(f"WARNING: Estimator yields invalid, non-positive predictions "
f" for {n_masked} samples out of {n_samples}. These predictions "
f"are ignored when computing the Poisson deviance.")
print("mean Poisson deviance: %.3f" %
mean_poisson_deviance(df_test["Frequency"][mask],
y_pred[mask],
sample_weight=df_test["Exposure"][mask]))
print("Constant mean frequency evaluation:")
score_estimator(dummy, df_test)
Constant mean frequency evaluation:
MSE: 0.564
MAE: 0.189
mean Poisson deviance: 0.625
(广义)线性模型
我们首先用(L2惩罚的)最小二乘线性回归模型对目标变量进行建模，这一模型被称为岭回归(Ridge回归)。我们使用一个低惩罚 alpha，因为我们料想这样的线性模型不适合在如此大的数据集。
from sklearn.linear_model import Ridge
ridge_glm = Pipeline([
("preprocessor", linear_model_preprocessor),
("regressor", Ridge(alpha=1e-6)),
]).fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
泊松偏差不能用模型预测的非正值来计算。对于返回一些非正预测(如岭回归)的模型，我们忽略相应的样本，这意味着所获得的泊松偏差是近似的。另一种方法是使用TransformedTargetRegressor元估计器将y_pred映射到严格正域。
print("Ridge evaluation:")
score_estimator(ridge_glm, df_test)
Ridge evaluation:
MSE: 0.560
MAE: 0.177
WARNING: Estimator yields invalid, non-positive predictions for 1315 samples out of 223745. These predictions are ignored when computing the Poisson deviance.
mean Poisson deviance: 0.601
接下来，我们对目标变量上拟合Poisson回归。
我们将正则化强度 alpha 设为样本数(1e-12)上的约1e-6，以模拟L2惩罚项与样本数不同的岭回归。
由于Poisson回归器内部模拟的是期望目标值的对数，而不是直接的期望值(log vs identity link function)，所以X和y之间的关系不再完全是线性的.因此，Poisson回归被称为广义线性模型(GLM)，而不是岭回归的一般线性模型。
from sklearn.linear_model import PoissonRegressor
n_samples = df_train.shape[0]
poisson_glm = Pipeline([
("preprocessor", linear_model_preprocessor),
("regressor", PoissonRegressor(alpha=1e-12, max_iter=300))
])
poisson_glm.fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
print("PoissonRegressor evaluation:")
score_estimator(poisson_glm, df_test)
PoissonRegressor evaluation:
MSE: 0.560
MAE: 0.186
mean Poisson deviance: 0.594
Poisson回归的梯度提升回归树
最后，我们将考虑一个非线性模型，即梯度提升回归树。基于树的模型不需要对分类数据进行独热编码：相反，我们可以使用OrdinalEncoder对每个类别标签进行任意整数的编码。通过这种编码，树将把分类特征视为有序的特征，这可能并不总是期望的行为。然而，对于能够恢复特征分类性质的足够深的树，这种效果是有限的。 OrdinalEncoder的主要优点是它将使训练速度比 OneHotEncoder更快。
梯度提升还提供了用泊松损失(用 implicit log-link function)来拟合树的可能性，而不是默认的最小二乘损失。在这里，为了保持这个例子的简洁，我们只用Poisson损失来拟合树。
from sklearn.experimental import enable_hist_gradient_boosting # noqa
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.preprocessing import OrdinalEncoder
tree_preprocessor = ColumnTransformer(
[
("categorical", OrdinalEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
("numeric", "passthrough",
["VehAge", "DrivAge", "BonusMalus", "Density"]),
],
remainder="drop",
)
poisson_gbrt = Pipeline([
("preprocessor", tree_preprocessor),
("regressor", HistGradientBoostingRegressor(loss="poisson",
max_leaf_nodes=128)),
])
poisson_gbrt.fit(df_train, df_train["Frequency"],
regressor__sample_weight=df_train["Exposure"])
print("Poisson Gradient Boosted Trees evaluation:")
score_estimator(poisson_gbrt, df_test)
Poisson Gradient Boosted Trees evaluation:
MSE: 0.560
MAE: 0.184
mean Poisson deviance: 0.575
与上面的Poisson GLM模型一样，梯度提升树模型使泊松偏差最小化。然而，由于其较高的预测能力，其泊松偏差值较低。
单一训练/测试分离的评估模型容易受到随机波动的影响。如果计算资源允许，应该使用交叉验证的性能指标， 但是将导致类似的结论。
通过比较观察到的目标值和预测值的直方图，也可以看到这些模型之间的定性差异：
fig, axes = plt.subplots(nrows=2, ncols=4, figsize=(16, 6), sharey=True)
fig.subplots_adjust(bottom=0.2)
n_bins = 20
for row_idx, label, df in zip(range(2),
["train", "test"],
[df_train, df_test]):
df["Frequency"].hist(bins=np.linspace(-1, 30, n_bins),
ax=axes[row_idx, 0])
axes[row_idx, 0].set_title("Data")
axes[row_idx, 0].set_yscale('log')
axes[row_idx, 0].set_xlabel("y (observed Frequency)")
axes[row_idx, 0].set_ylim([1e1, 5e5])
axes[row_idx, 0].set_ylabel(label + " samples")
for idx, model in enumerate([ridge_glm, poisson_glm, poisson_gbrt]):
y_pred = model.predict(df)
pd.Series(y_pred).hist(bins=np.linspace(-1, 4, n_bins),
ax=axes[row_idx, idx+1])
axes[row_idx, idx + 1].set(
title=model[-1].__class__.__name__,
yscale='log',
xlabel="y_pred (predicted expected Frequency)"
)
plt.tight_layout()
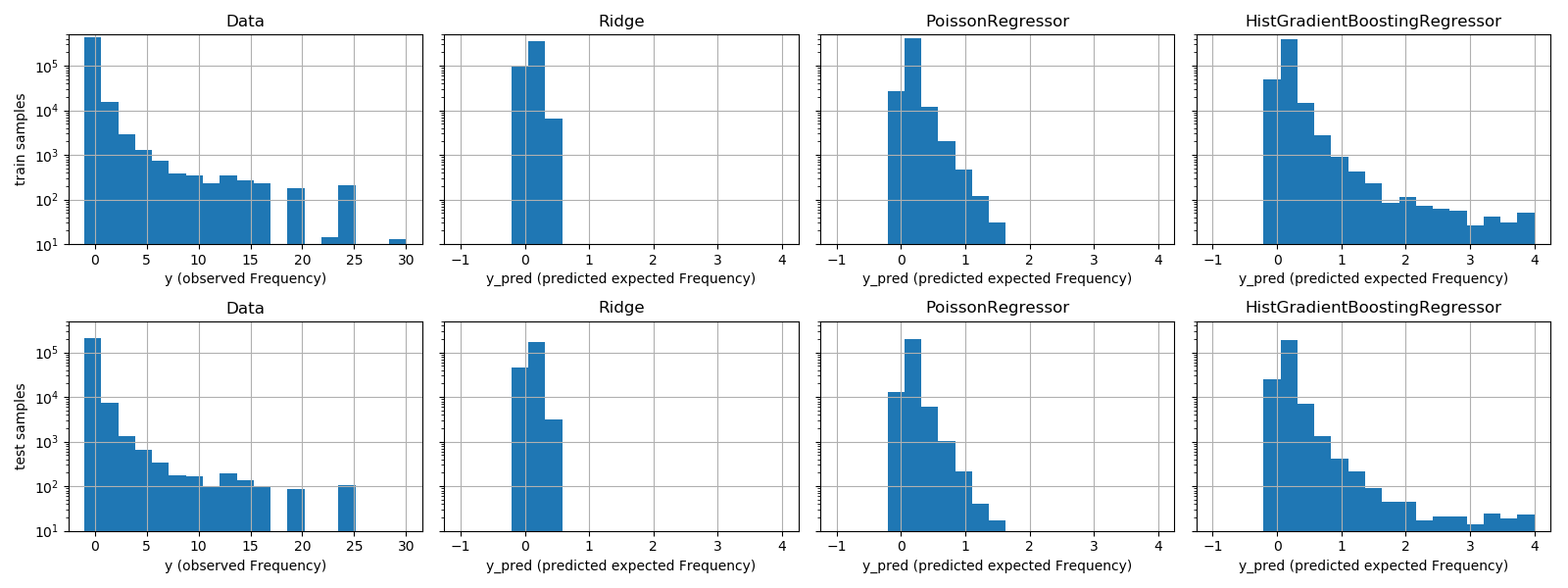实验数据给出了y的长尾分布。在所有模型中，我们都预测了随机变量的期望频率，因此，与观察到的该随机变量的实现相比，我们的极值必然会更少。这解释了模型预测直方图的模式不一定与最小值相对应。另外，Ridge的正态分布具有恒定的方差，而PoissonRegressor和定GradientBoostingRegressor的Poisson分布的方差与预测的期望值成正比。
因此，在所考虑的估计器中，PoissonRegressor和组GRadientBoostingRegressor比Ridge模型更适合于模拟非负数据的长尾分布，而岭模型对目标变量的分布作了错误的假设。
HistGradientBoostingRegressor估计器具有最大的灵活性，能够预测较高的期望值。
请注意，我们可以对GRadientBoostingRegressor模型使用最小二乘损失。这将错误地假设一个正常分布的响应变量，就像Ridge模型一样，而且可能还会导致轻微的负面预测。然而，由于树的灵活性，加上大量的训练样本，梯度提升树仍然表现得比较好，特别是比PoissonRegressor更好。
对预测校准的评估
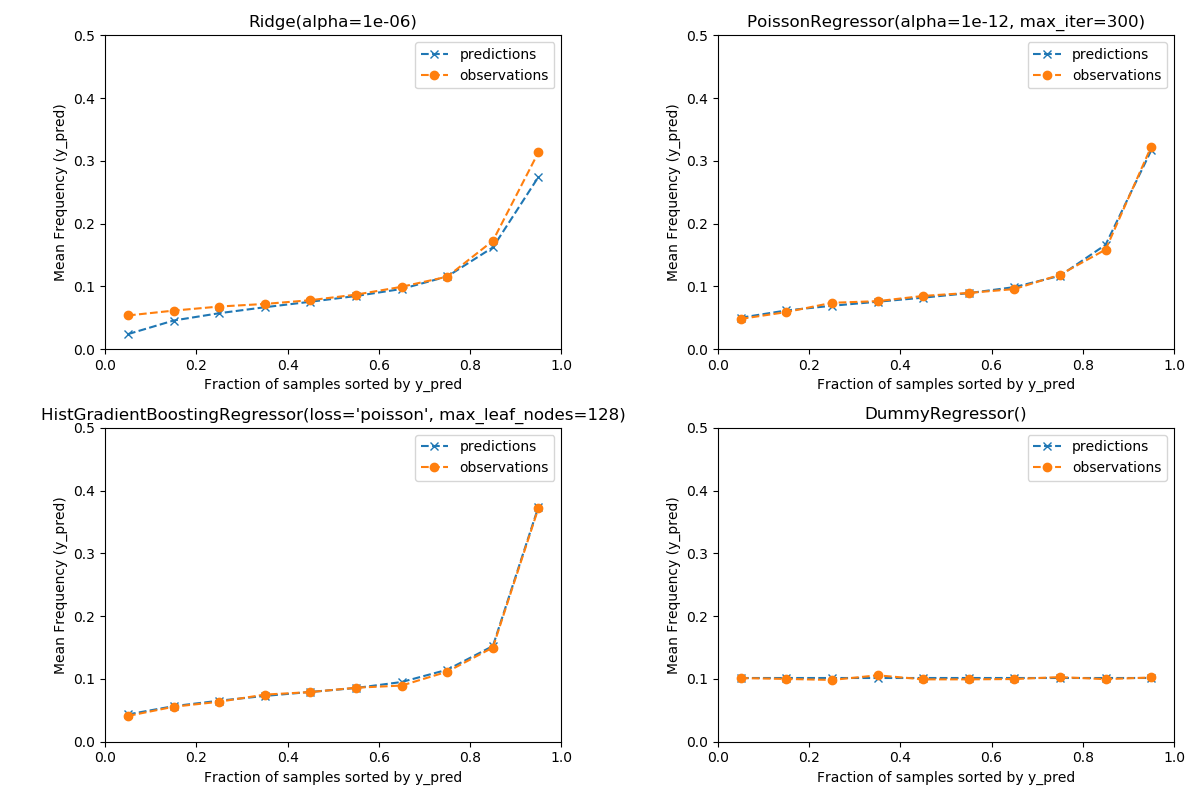
为了保证估计器对不同的投保人类型做出合理的预测，我们可以根据每个模型返回的y_pred来装箱测试样本。然后，对于每个箱子，我们比较了预测的y_pred的平均值和平均观察到的目标得平均值：
from sklearn.utils import gen_even_slices
def _mean_frequency_by_risk_group(y_true, y_pred, sample_weight=None,
n_bins=100):
"""Compare predictions and observations for bins ordered by y_pred.
We order the samples by ``y_pred`` and split it in bins.
In each bin the observed mean is compared with the predicted mean.
Parameters
----------
y_true: array-like of shape (n_samples,)
Ground truth (correct) target values.
y_pred: array-like of shape (n_samples,)
Estimated target values.
sample_weight : array-like of shape (n_samples,)
Sample weights.
n_bins: int
Number of bins to use.
Returns
-------
bin_centers: ndarray of shape (n_bins,)
bin centers
y_true_bin: ndarray of shape (n_bins,)
average y_pred for each bin
y_pred_bin: ndarray of shape (n_bins,)
average y_pred for each bin
"""
idx_sort = np.argsort(y_pred)
bin_centers = np.arange(0, 1, 1/n_bins) + 0.5/n_bins
y_pred_bin = np.zeros(n_bins)
y_true_bin = np.zeros(n_bins)
for n, sl in enumerate(gen_even_slices(len(y_true), n_bins)):
weights = sample_weight[idx_sort][sl]
y_pred_bin[n] = np.average(
y_pred[idx_sort][sl], weights=weights
)
y_true_bin[n] = np.average(
y_true[idx_sort][sl],
weights=weights
)
return bin_centers, y_true_bin, y_pred_bin
print(f"Actual number of claims: {df_test['ClaimNb'].sum()}")
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(12, 8))
plt.subplots_adjust(wspace=0.3)
for axi, model in zip(ax.ravel(), [ridge_glm, poisson_glm, poisson_gbrt,
dummy]):
y_pred = model.predict(df_test)
y_true = df_test["Frequency"].values
exposure = df_test["Exposure"].values
q, y_true_seg, y_pred_seg = _mean_frequency_by_risk_group(
y_true, y_pred, sample_weight=exposure, n_bins=10)
# Name of the model after the estimator used in the last step of the
# pipeline.
print(f"Predicted number of claims by {model[-1]}: "
f"{np.sum(y_pred * exposure):.1f}")
axi.plot(q, y_pred_seg, marker='x', linestyle="--", label="predictions")
axi.plot(q, y_true_seg, marker='o', linestyle="--", label="observations")
axi.set_xlim(0, 1.0)
axi.set_ylim(0, 0.5)
axi.set(
title=model[-1],
xlabel='Fraction of samples sorted by y_pred',
ylabel='Mean Frequency (y_pred)'
)
axi.legend()
plt.tight_layout()
Actual number of claims: 11935.0
Predicted number of claims by Ridge(alpha=1e-06): 10692.9
Predicted number of claims by PoissonRegressor(alpha=1e-12, max_iter=300): 11928.3
Predicted number of claims by HistGradientBoostingRegressor(loss='poisson', max_leaf_nodes=128): 12109.6
Predicted number of claims by DummyRegressor(): 11931.2
虚拟回归模型预测一个恒定的频率。这个模型并没有将所有样本都归为相同的约束等级，而是在全部范围内得到了很好的校准(以估计整个人口的平均频率)。
岭回归模型可以预测与数据不匹配的非常低的期望频率。因此，这可能会严重低估某些投保人的风险。
PoissonRegressor和组织GradientBoostingRegressor在预测目标和观察目标之间表现出较好的一致性，特别是对于低预测目标值。
所有预测的总和也证实了岭模型的校准问题：它低估了测试集中索赔总数的3%以上，而其他三种模型可以大致恢复测试组合的索赔总数。
排名权的评估
对于某些业务应用，我们感兴趣的是，无论预测的绝对值如何，模型是否能够从最安全的投保人中对风险进行排序。在这种情况下，模型评估会将问题描述为排序问题，而不是回归问题。
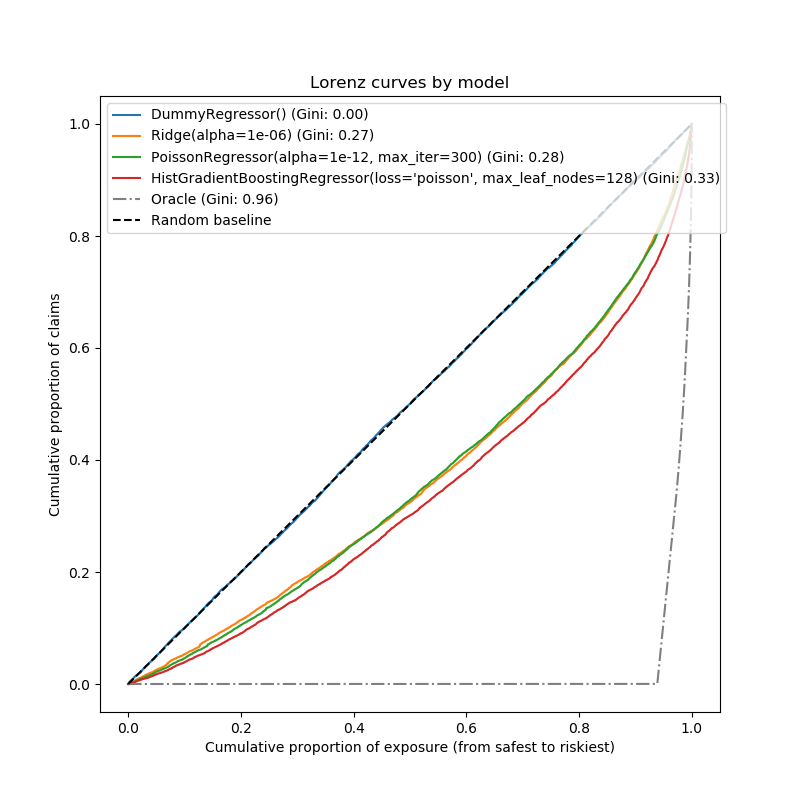
为了从这个角度比较这三个模型，我们可以根据模型的预测，从最安全到最危险的模型预测，绘制索赔的累积比例与测试样本顺序的累积暴露比例。
这幅图被称为Lorenz曲线，可以用基尼指数来概括：
from sklearn.metrics import auc
def lorenz_curve(y_true, y_pred, exposure):
y_true, y_pred = np.asarray(y_true), np.asarray(y_pred)
exposure = np.asarray(exposure)
# order samples by increasing predicted risk:
ranking = np.argsort(y_pred)
ranked_exposure = exposure[ranking]
ranked_frequencies = y_true[ranking]
ranked_exposure = exposure[ranking]
cumulated_claims = np.cumsum(ranked_frequencies * ranked_exposure)
cumulated_claims /= cumulated_claims[-1]
cumulated_exposure = np.cumsum(ranked_exposure)
cumulated_exposure /= cumulated_exposure[-1]
return cumulated_exposure, cumulated_claims
fig, ax = plt.subplots(figsize=(8, 8))
for model in [dummy, ridge_glm, poisson_glm, poisson_gbrt]:
y_pred = model.predict(df_test)
cum_exposure, cum_claims = lorenz_curve(df_test["Frequency"], y_pred,
df_test["Exposure"])
gini = 1 - 2 * auc(cum_exposure, cum_claims)
label = "{} (Gini: {:.2f})".format(model[-1], gini)
ax.plot(cum_exposure, cum_claims, linestyle="-", label=label)
# Oracle model: y_pred == y_test
cum_exposure, cum_claims = lorenz_curve(df_test["Frequency"],
df_test["Frequency"],
df_test["Exposure"])
gini = 1 - 2 * auc(cum_exposure, cum_claims)
label = "Oracle (Gini: {:.2f})".format(gini)
ax.plot(cum_exposure, cum_claims, linestyle="-.", color="gray", label=label)
# Random Baseline
ax.plot([0, 1], [0, 1], linestyle="--", color="black",
label="Random baseline")
ax.set(
title="Lorenz curves by model",
xlabel='Cumulative proportion of exposure (from safest to riskiest)',
ylabel='Cumulative proportion of claims'
)
ax.legend(loc="upper left")
<matplotlib.legend.Legend object at 0x7f96079cbc10>
正如预期的那样，虚拟回归者无法正确地对样本进行排序，因此在此图上执行最糟糕的操作。
基于树的模型在按风险对投保人排序方面有明显的优势，而两个线性模型的表现类似。
这三种模型都明显优于偶然性，但也远未做出完美的预测。
由于问题的性质，预计这最后一点：事故的发生主要是间接原因，数据集中的列中没有捕捉到这些原因，而且确实可以认为是纯粹的随机因素。
线性模型假定输入变量之间不存在交互作用，这可能导致拟合不足。插入多项式特征提取器(PolynomialFeatures)确实使它们的描述能力增加了2点的基尼指数。特别是，它提高了模型识别前5%风险最大形象的能力。
Main takeaways
这些模型的性能可以通过它们能够做出精确的预测和良好的排名来评估。 该模型的标定可以通过被预测风险组合的测试样本的平均观测值和平均预测值来评估。 岭回归模型的最小二乘损失(以及识别链接函数的隐式使用)似乎导致该模型被严重校准。特别是，它往往低估风险，甚至可以预测无效的负频率。 使用带对数链的泊松损失可以纠正这些问题，并形成一个校正良好的线性模型。 基尼指数反映了一个模型无论其绝对值如何对预测进行排序的能力，因此只评估它们的排序能力。 尽管在校准方面有所改进，但两种线性模型的排序能力是相当的，并且远低于梯度提升回归树的排能力。 作为评价指标计算的泊松偏差既反映了模型的校准能力，又反映了模型的排序能力。它还对响应变量的期望值与方差之间的理想关系作了线性假设。为了简洁起见，我们没有检查这个假设是否成立。 传统的回归度量，如均方误差和平均绝对误差，很难对有很多0的计数值进行有意义的解释。
plt.show()
脚本的总运行时间：(1分0.675秒)
Download Python source code:plot_poisson_regression_non_normal_loss.py
Download Jupyter notebook:plot_poisson_regression_non_normal_loss.ipynb