线性模型系数解释中的常见缺陷¶

在线性模型中，目标值被建模为特征的线性组合(请参阅scikit-learn中“Linear Models 用户指南”一节中对一组可用的线性模型的描述)。多个线性模型中的系数表示给定特征与目标之间的关系，假设所有其他特征保持不变(条件依赖)。这与绘制对和拟合线性关系不同：在这种情况下，其他特征的所有可能值都会在估计中得到考虑(边际依赖)。

此示例将为解释线性模型中的系数提供一些提示，指出当线性模型不适合描述数据集或当特征相关时会出现的问题。

我们会利用1985年的“目前人口统计调查”的数据，根据经验、年龄或教育程度等各方面因素来预测工资。

• 数据集：工资
• 机器学习工作流
• 处理数据集
• 解释系数：尺度问题
• 检验系数的可变性
• 关联变量问题
• 预处理数值变量
• 正则化线性模型
• 稀疏系数的线性模型
• 课程学习

print(__doc__)

import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

数据集：工资

我们从OpenML获取数据。注意，将参数 as_frame 设置为True， 将以pandas数据的形式检索数据。

from sklearn.datasets import fetch_openml

survey = fetch_openml(data_id=534, as_frame=True)

然后，我们识别特征X和目标y：列WAGE是我们的目标变量(即我们想要预测的变量)。

X = survey.data[survey.feature_names]
X.describe(include="all")

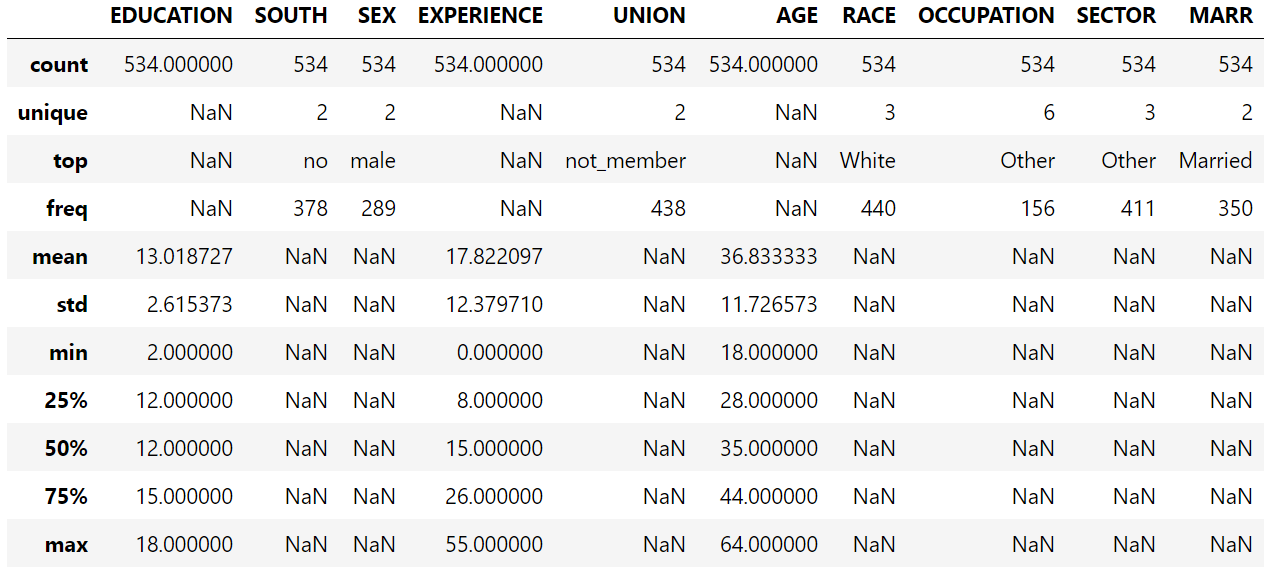注意，数据集包含分类变量和数值变量。在以后对数据集进行预处理时，我们需要考虑到这一点。

X.head()

我们的预测目标是：the wage。工资被描述为以每小时美元为单位的浮点数。

y = survey.target.values.ravel()
survey.target.head()

0    5.10
1    4.95
2    6.67
3    4.00
4    7.50
Name: WAGE, dtype: float64

我们将样本分解成一个训练集和一个测试集。只有训练数据集将用于以下探索性分析。这是一种模拟在未知目标上执行预测的真实情况的方法，我们不希望我们的分析和决定因我们对测试数据有所了解而有偏差。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, random_state=42
)

首先，让我们通过查看变量分布和它们之间的成对关系来获得一些洞察力。只数值变量被使用。在下面的图中，每个点表示一个示例。

train_dataset = X_train.copy()
train_dataset.insert(0, "WAGE", y_train)
_ = sns.pairplot(train_dataset, kind='reg', diag_kind='kde')

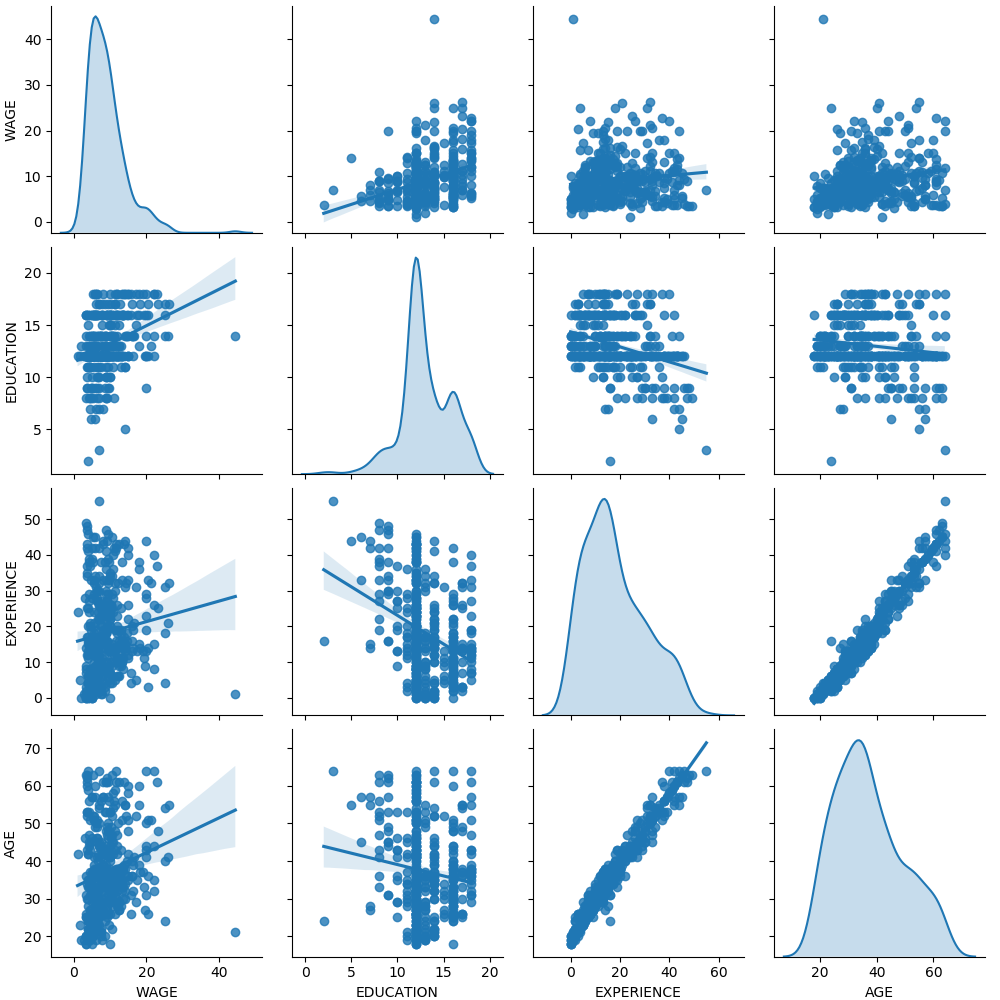仔细看一看工资分布，就会发现它是长尾的。因此，我们应该把它的对数近似地转化为正态分布(线性模型，如岭回归或Lasso最适合用于正态分布的误差)。

随着 EDUCATION 的增加，WAGE 在增加。请注意，这里表示的工资和教育之间的依赖是边际依赖，也就是说，它描述了一个特定变量的行为，而没有保持其他变量的固定。

此外，EXPERIENCE 与 AGE 呈高度线性相关。

机器学习工作流

为了设计机器学习管道，我们首先手动检查需要处理的数据类型：

survey.data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 534 entries, 0 to 533
Data columns (total 10 columns):
 #   Column      Non-Null Count  Dtype
---  ------      --------------  -----
 0   EDUCATION   534 non-null    float64
 1   SOUTH       534 non-null    category
 2   SEX         534 non-null    category
 3   EXPERIENCE  534 non-null    float64
 4   UNION       534 non-null    category
 5   AGE         534 non-null    float64
 6   RACE        534 non-null    category
 7   OCCUPATION  534 non-null    category
 8   SECTOR      534 non-null    category
 9   MARR        534 non-null    category
dtypes: category(7), float64(3)
memory usage: 17.1 KB

如前所述，数据集包含具有不同数据类型的列，我们需要对每个数据类型应用特定的预处理。特别是，如果分类变量不首先编码为整数，则不能将分类变量包括在线性模型中。此外，为了避免将分类特征视为有序值，我们需要对它们进行一次独热编码。我们的预处理器：

• 独热编码(即按类别生成一列)分类列；
• 作为第一种方法(我们将看到数值的标准化将如何影响我们的讨论)，保持数值的原样。

from sklearn.compose import make_column_transformer
from sklearn.preprocessing import OneHotEncoder

categorical_columns = ['RACE', 'OCCUPATION', 'SECTOR',
                       'MARR', 'UNION', 'SEX', 'SOUTH']
numerical_columns = ['EDUCATION', 'EXPERIENCE', 'AGE']

preprocessor = make_column_transformer(
    (OneHotEncoder(drop='if_binary'), categorical_columns),
    remainder='passthrough'
)

为了将数据集描述为线性模型，我们使用了一个正则化程度很小的岭回归，并对WAGE的对数进行了建模。

from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Ridge
from sklearn.compose import TransformedTargetRegressor

model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=Ridge(alpha=1e-10),
        func=np.log10,
        inverse_func=sp.special.exp10
    )
)

处理数据集

首先，我们拟合模型。

_ = model.fit(X_train, y_train)

然后，我们检查计算模型的性能，绘制它在测试集上的预测，并计算，例如，模型的中位绝对误差。

from sklearn.metrics import median_absolute_error

y_pred = model.predict(X_train)

mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'
fig, ax = plt.subplots(figsize=(5, 5))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")
plt.text(3, 20, string_score)
plt.title('Ridge model, small regularization')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])

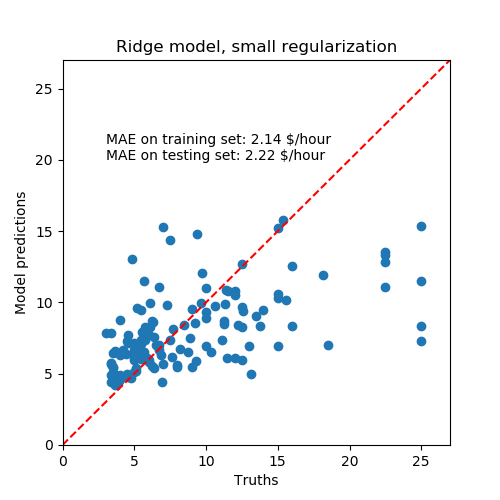学习到的模型远不是一个做出准确预测的好模型：从上面的情节来看，这是显而易见的，在那里，好的预测应该在红线上。

在下一节中，我们将解释模型的系数。当我们这样做的时候，我们应该记住，我们得出的任何结论都是关于我们建立的模型，而不是关于数据的真实(现实世界)生成过程。

解释系数：尺度问题

首先，我们可以查看我们所拟合的回归系数的值。

feature_names = (model.named_steps['columntransformer']
                      .named_transformers_['onehotencoder']
                      .get_feature_names(input_features=categorical_columns))
feature_names = np.concatenate(
    [feature_names, numerical_columns])

coefs = pd.DataFrame(
    model.named_steps['transformedtargetregressor'].regressor_.coef_,
    columns=['Coefficients'], index=feature_names
)

coefs

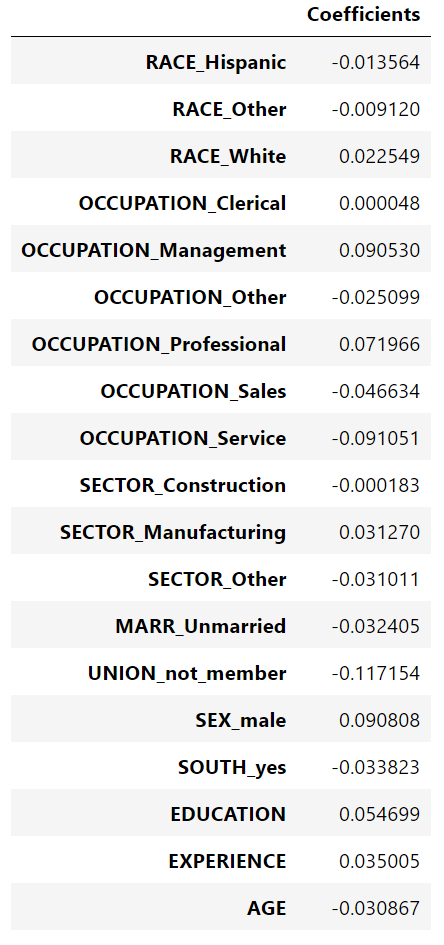年龄系数以“每活一年美元/小时”表示，而教育系数则以“每受教育一年美元/小时”表示。这个系数的表示说明了模型的实际预测：1岁的增长意味着每小时减少0.030867美元，而1年的教育增长意味着每小时增加0.054699美元。另一方面，范畴变量(如联合变量或性别变量)是取值0或1的维数，其系数以美元/小时表示。然后，由于特征的度量单位不同，因此不能比较不同系数的大小，因为它们具有不同的自然尺度，因而具有不同的取值范围。如果我们绘制系数，这是更明显的。

coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, small regularization')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)

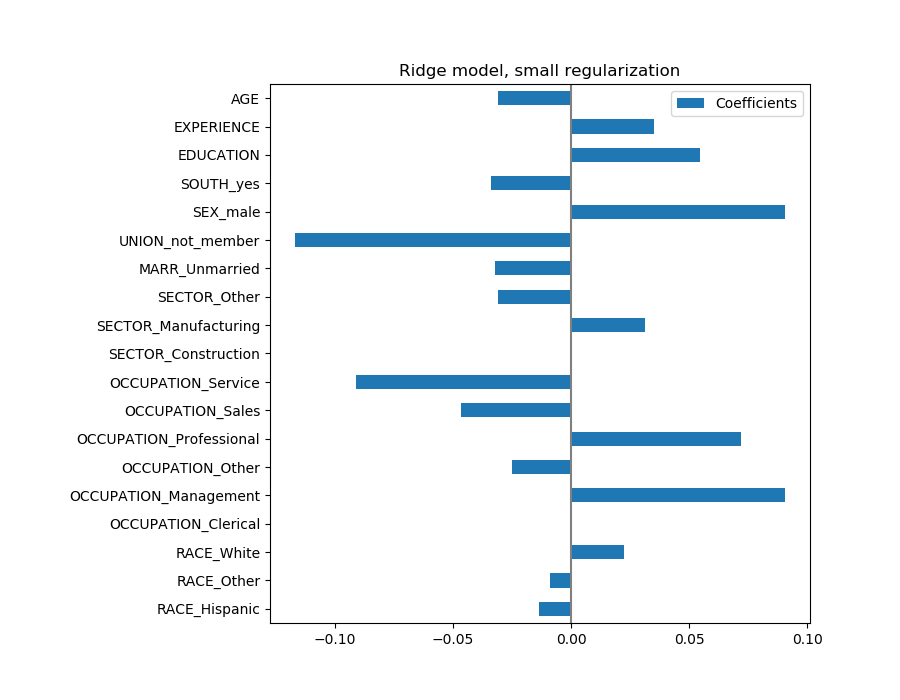事实上，从上面的图来看，决定WAGE的最重要因素似乎是UNION，即使我们的直觉可能告诉我们，像 EXPERIENCE这样的变量应该有更大的影响。

观察系数图来衡量特征的重要性可能会产生误导，因为其中一些变化很小，而另一些，如AGE，变化更大，甚至几十年。

如果我们比较不同特征的标准差，这是可见的。

X_train_preprocessed = pd.DataFrame(
    model.named_steps['columntransformer'].transform(X_train),
    columns=feature_names
)

X_train_preprocessed.std(axis=0).plot(kind='barh', figsize=(9, 7))
plt.title('Features std. dev.')
plt.subplots_adjust(left=.3)

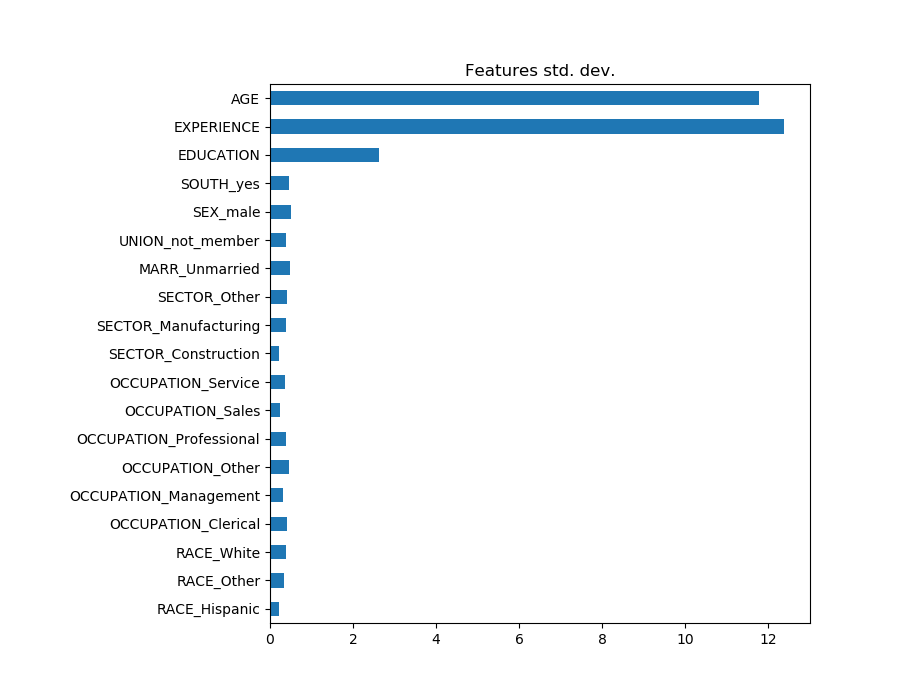将系数乘以相关特征的标准差，将所有系数减少到相同的度量单位。我们将看到，这相当于将数值变量标准化为其标准差，如:

在这种情况下，我们强调，特征的方差越大，输出的相应系数的权重就越大，所有这些都是相等的。

coefs = pd.DataFrame(
    model.named_steps['transformedtargetregressor'].regressor_.coef_ *
    X_train_preprocessed.std(axis=0),
    columns=['Coefficient importance'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, small regularization')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)

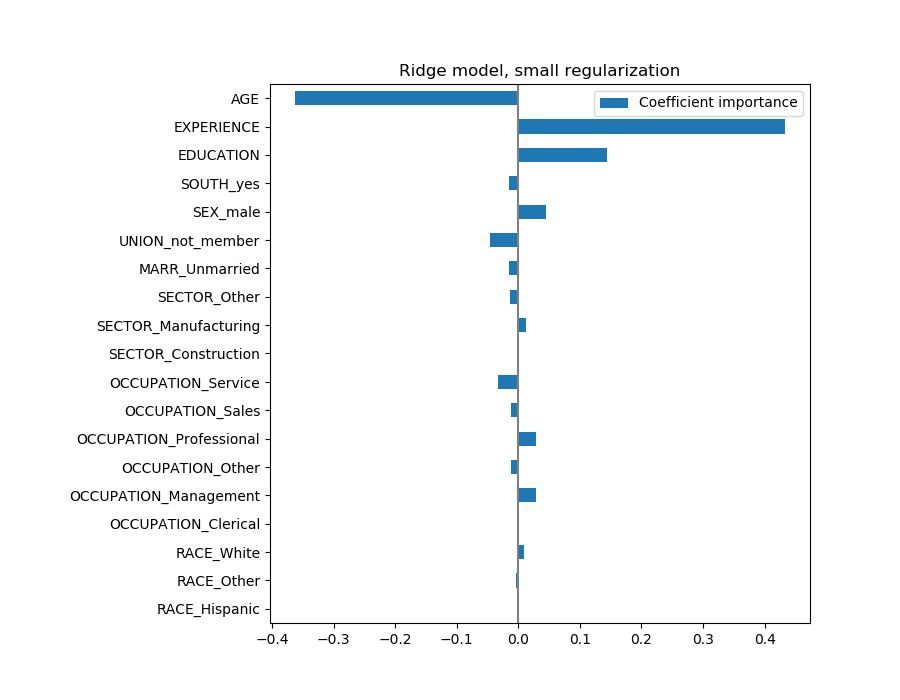现在系数已经被缩放了，我们可以安全地比较它们。

警告：为什么上面的情节意味着年龄的增长会导致工资的下降？为什么 initial pairplot告诉我们相反的情况？

上面的图告诉我们，当所有其他特性保持不变(即条件依赖关系)时，特定特性与目标之间的依赖关系。即：条件依赖。当所有其他特征不变时，年龄的增加将导致工资的下降。相反，当所有其他特征不变时，经验的增加会导致工资的增加。此外，年龄、经验和教育是对模型影响最大的三个变量。

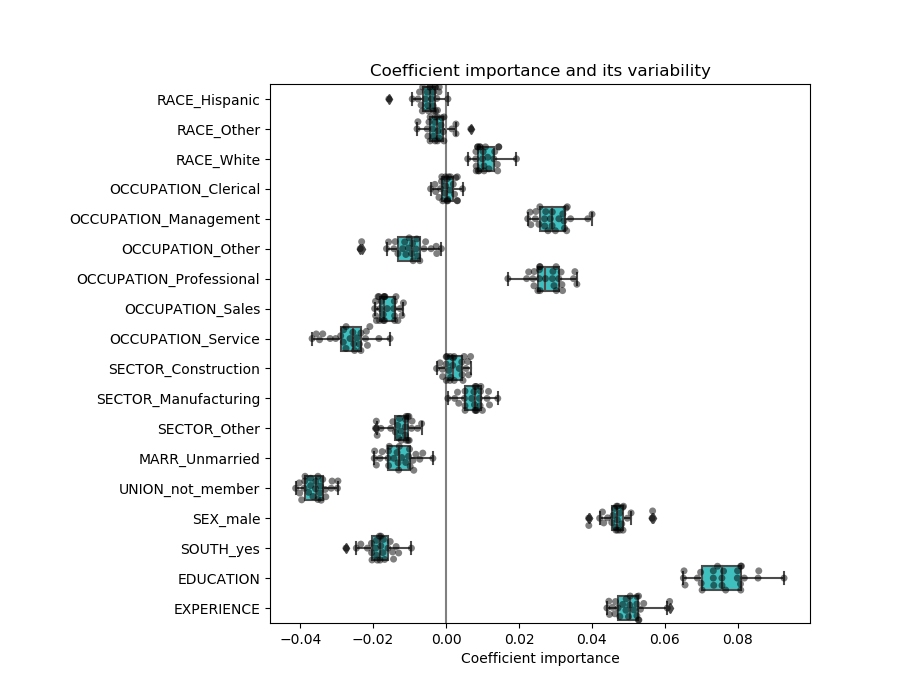
检验系数的可变性

我们可以通过交叉验证来检验系数的可变性：它是数据扰动的一种形式(与重采样有关)。

如果系数在改变输入数据集时变化很大，则不能保证它们的鲁棒性，因此很可能需要谨慎地解释它们。

from sklearn.model_selection import cross_validate
from sklearn.model_selection import RepeatedKFold

cv_model = cross_validate(
    model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
    return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
    [est.named_steps['transformedtargetregressor'].regressor_.coef_ *
     X_train_preprocessed.std(axis=0)
     for est in cv_model['estimator']],
    columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.swarmplot(data=coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.xlabel('Coefficient importance')
plt.title('Coefficient importance and its variability')
plt.subplots_adjust(left=.3)

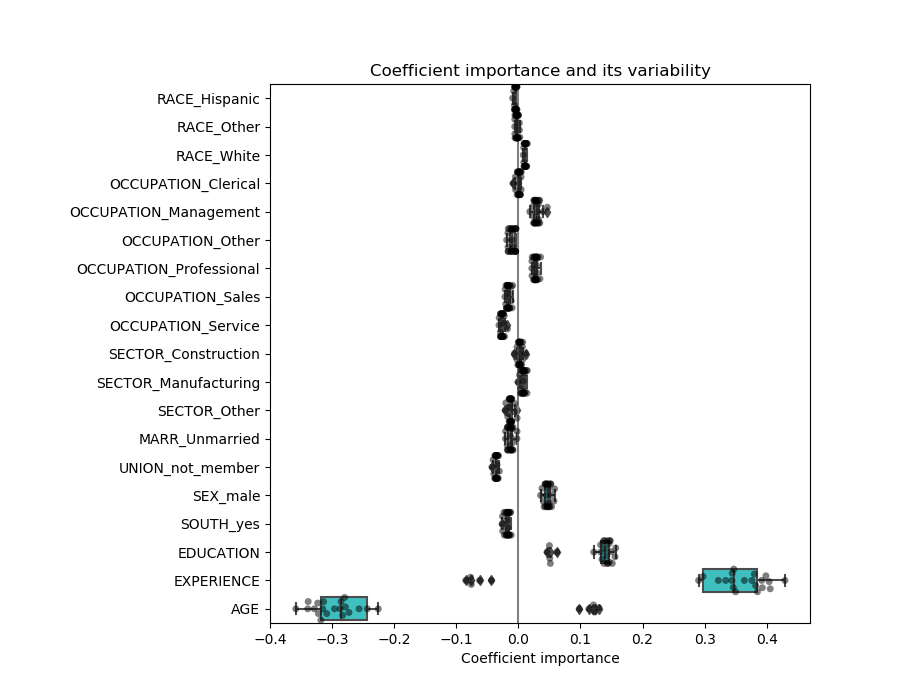
关联变量问题

AGE和EXPERIENCE 系数受强变异性的影响，这可能是由于这两个特征之间的共线性所致：由于AGE和EXPERIENCE在数据中的差异，它们的影响很难分开。

为了验证这一解释，我们绘制了年龄和经验系数的变异性图。

plt.ylabel('Age coefficient')
plt.xlabel('Experience coefficient')
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title('Co-variations of coefficients for AGE and EXPERIENCE '
              'across folds')

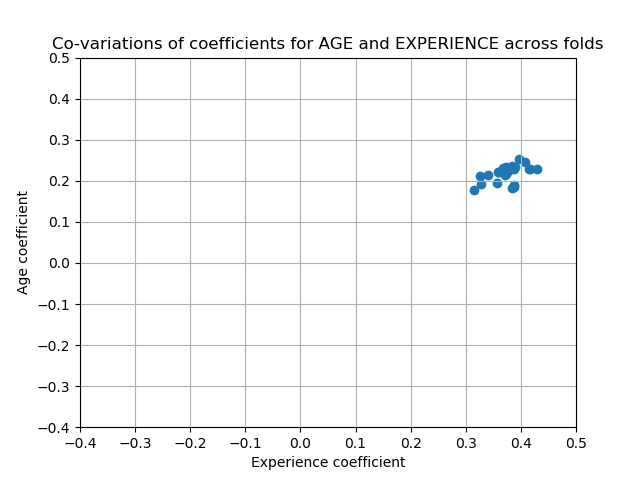
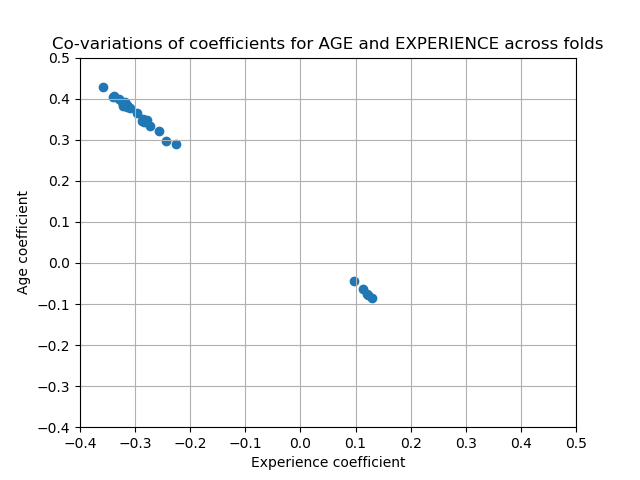有两个区域：当EXPERIENCE系数为正值时，AGE为负，反之亦然。

为了更进一步，我们删除了这两个特征中的一个，并检查了对模型稳定性的影响。

column_to_drop = ['AGE']

cv_model = cross_validate(
    model, X.drop(columns=column_to_drop), y,
    cv=RepeatedKFold(n_splits=5, n_repeats=5),
    return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
    [est.named_steps['transformedtargetregressor'].regressor_.coef_ *
     X_train_preprocessed.drop(columns=column_to_drop).std(axis=0)
     for est in cv_model['estimator']],
    columns=feature_names[:-1]
)
plt.figure(figsize=(9, 7))
sns.swarmplot(data=coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.title('Coefficient importance and its variability')
plt.xlabel('Coefficient importance')
plt.subplots_adjust(left=.3)

经验系数的估计现在变小了，对所有在交叉验证过程中训练的模型仍然很重要。

预处理数值变量

如前所述(请参阅“机器学习工作流”)，我们也可以选择在训练模型之前缩放数值。这将有助于将类似的数量正则化应用于岭中的所有。为了将均值和尺度变化减去单位方差，对预处理器进行了重新定义。

from sklearn.preprocessing import StandardScaler

preprocessor = make_column_transformer(
    (OneHotEncoder(drop='if_binary'), categorical_columns),
    (StandardScaler(), numerical_columns),
    remainder='passthrough'
)

模型将保持不变。

model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=Ridge(alpha=1e-10),
        func=np.log10,
        inverse_func=sp.special.exp10
    )
)

_ = model.fit(X_train, y_train)

再次，我们用模型的中位绝对误差和R方系数来检验计算模型的性能。

y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'
fig, ax = plt.subplots(figsize=(6, 6))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")

plt.text(3, 20, string_score)

plt.title('Ridge model, small regularization, normalized variables')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])

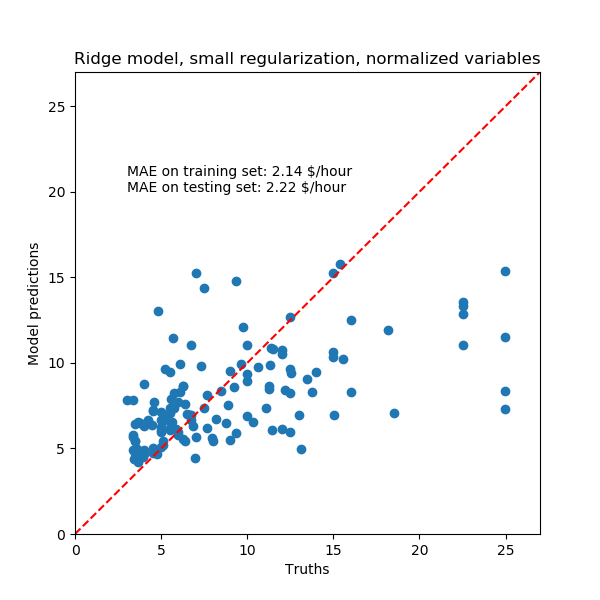对于系数分析，这次不需要缩放。

coefs = pd.DataFrame(
    model.named_steps['transformedtargetregressor'].regressor_.coef_,
    columns=['Coefficients'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, small regularization, normalized variables')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)

我们现在检查几个交叉验证的系数。

cv_model = cross_validate(
    model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
    return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
    [est.named_steps['transformedtargetregressor'].regressor_.coef_
     for est in cv_model['estimator']],
    columns=feature_names
)
plt.figure(figsize=(9, 7))
sns.swarmplot(data=coefs, orient='h', color='k', alpha=0.5)
sns.boxplot(data=coefs, orient='h', color='cyan', saturation=0.5)
plt.axvline(x=0, color='.5')
plt.title('Coefficient variability')
plt.subplots_adjust(left=.3)

结果与非归一化情况十分相似。

正则化线性模型

在机器学习实践中，岭回归更常用于不可忽略的正则化。

上面，我们把这个正规化限制在很小的数量上。正则化改善了问题的条件，减少了估计的方差。RidgeCV应用交叉验证来确定正则化参数(Alpha)的哪个值最适合于预测。

from sklearn.linear_model import RidgeCV

model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=RidgeCV(alphas=np.logspace(-10, 10, 21)),
        func=np.log10,
        inverse_func=sp.special.exp10
    )
)

_ = model.fit(X_train, y_train)

首先，我们检查选择了哪个值的α。

model[-1].regressor_.alpha_

然后我们检查预测的质量。

y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'

fig, ax = plt.subplots(figsize=(6, 6))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")

plt.text(3, 20, string_score)

plt.title('Ridge model, regularization, normalized variables')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])

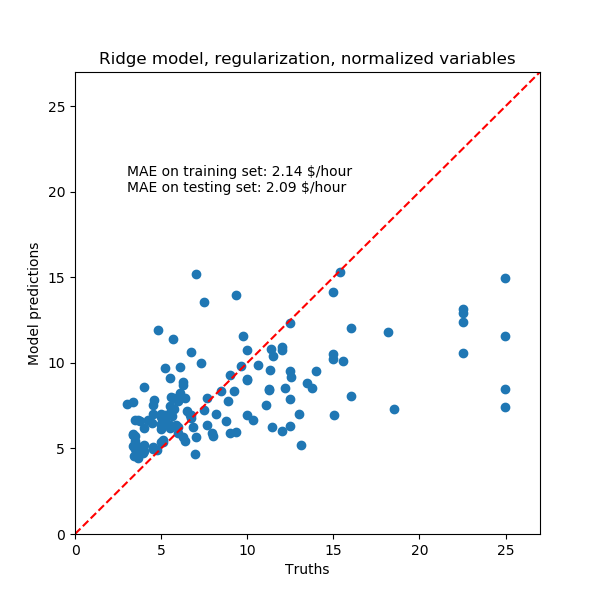正则化模型的数据再现能力与非正则模型相似。

coefs = pd.DataFrame(
    model.named_steps['transformedtargetregressor'].regressor_.coef_,
    columns=['Coefficients'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Ridge model, regularization, normalized variables')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)

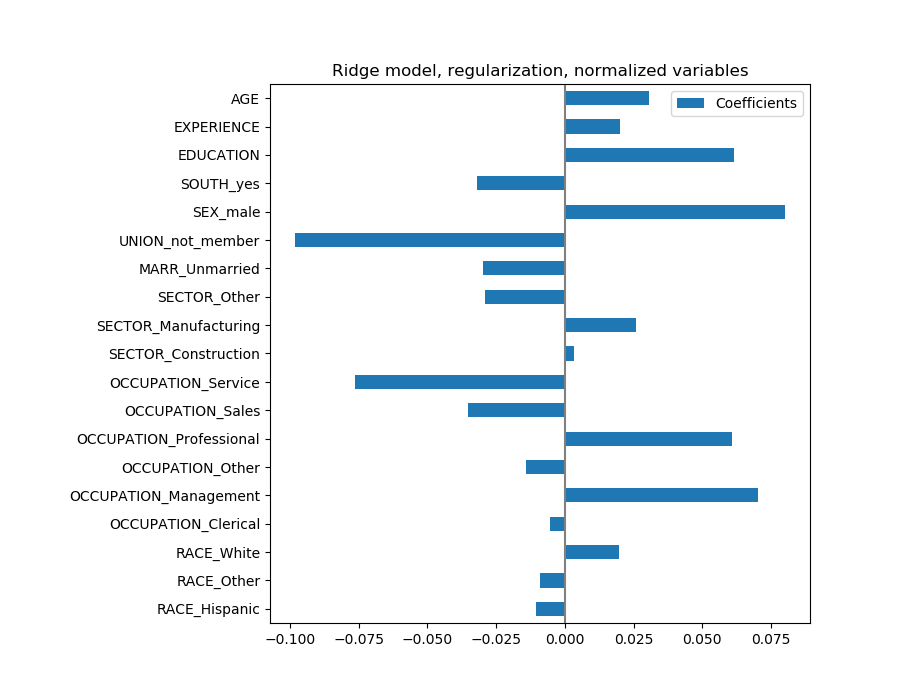这些系数有显着性差异。年龄和经验系数都是正的，但它们现在对预测的影响较小。

正则化减少了相关变量对模型的影响，因为权重在两个预测变量之间是共享的，因此两者都不会有很强的权重。

另一方面，正则化获得的权重更稳定(参见岭回归和分类用户指南一节)。在交叉验证中，从从数据扰动中获得的图中可以看出这种增加的稳定性。这个图可以和前一个相比较。

cv_model = cross_validate(
    model, X, y, cv=RepeatedKFold(n_splits=5, n_repeats=5),
    return_estimator=True, n_jobs=-1
)
coefs = pd.DataFrame(
    [est.named_steps['transformedtargetregressor'].regressor_.coef_ *
     X_train_preprocessed.std(axis=0)
     for est in cv_model['estimator']],
    columns=feature_names
)

plt.ylabel('Age coefficient')
plt.xlabel('Experience coefficient')
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title('Co-variations of coefficients for AGE and EXPERIENCE '
              'across folds')

稀疏系数的线性模型

在数据集中考虑相关变量的另一种可能性是估计稀疏系数。在某种程度上，当我们在以前的岭估计中删除AGE列时，我们已经手动完成了。

LASSO模型(见Lasso用户指南部分)估计稀疏系数。LassoCV应用交叉验证来确定正则化参数(Alpha)的哪个值最适合于模型估计。

from sklearn.linear_model import LassoCV

model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=LassoCV(alphas=np.logspace(-10, 10, 21), max_iter=100000),
        func=np.log10,
        inverse_func=sp.special.exp10
    )
)

_ = model.fit(X_train, y_train)

首先，我们检查了选择了哪个值的α。

model[-1].regressor_.alpha_

0.001

然后我们检查预测的质量。

y_pred = model.predict(X_train)
mae = median_absolute_error(y_train, y_pred)
string_score = f'MAE on training set: {mae:.2f} $/hour'
y_pred = model.predict(X_test)
mae = median_absolute_error(y_test, y_pred)
string_score += f'\nMAE on testing set: {mae:.2f} $/hour'

fig, ax = plt.subplots(figsize=(6, 6))
plt.scatter(y_test, y_pred)
ax.plot([0, 1], [0, 1], transform=ax.transAxes, ls="--", c="red")

plt.text(3, 20, string_score)

plt.title('Lasso model, regularization, normalized variables')
plt.ylabel('Model predictions')
plt.xlabel('Truths')
plt.xlim([0, 27])
_ = plt.ylim([0, 27])

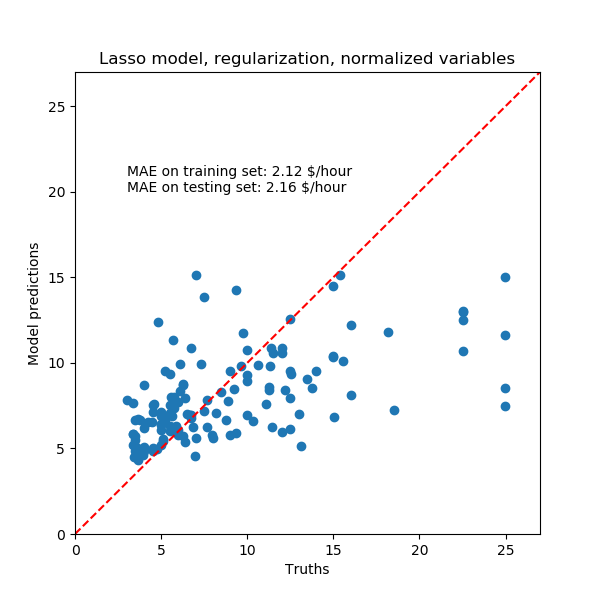同样，对于我们的数据集，模型也不是很有预见性。

coefs = pd.DataFrame(
    model.named_steps['transformedtargetregressor'].regressor_.coef_,
    columns=['Coefficients'], index=feature_names
)
coefs.plot(kind='barh', figsize=(9, 7))
plt.title('Lasso model, regularization, normalized variables')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)

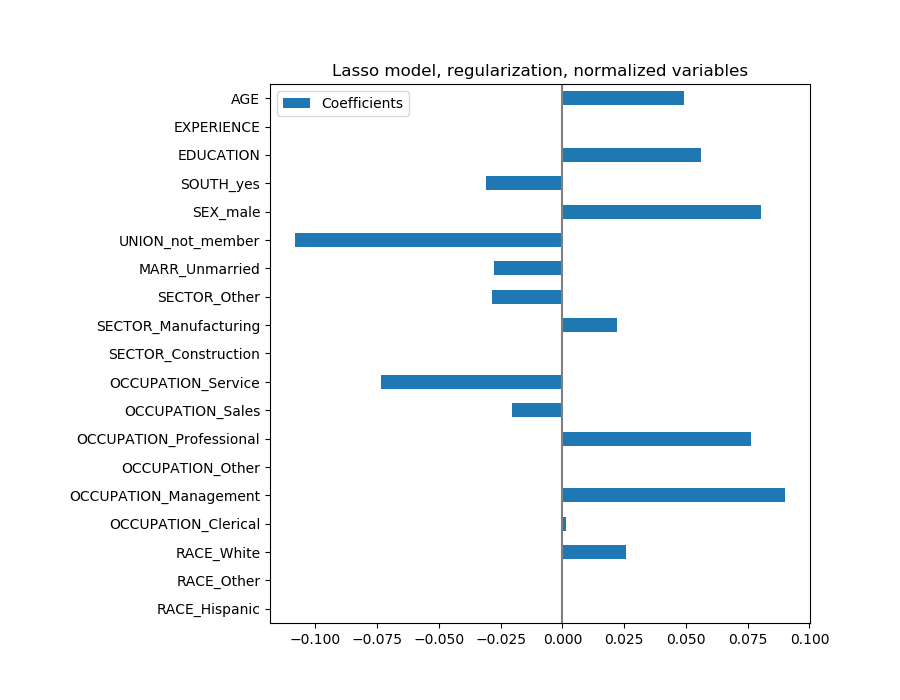Lasso模型识别了年龄和经验之间的相关性，并为了预测而压制其中一个。

重要的是要记住，被丢弃的系数可能仍然与结果本身有关：模型选择了抑制它们，因为它们在其他特征之上很少或没有额外的信息。

课程学习

• 要检索特征重要性，系数必须缩放到相同的度量单位。使用特性的标准差对它们进行缩放是一个有用的代理。
• 多元线性模型中的系数表示给定特征与目标之间的依赖关系，这有赖于其他特征。
• 相关特征导致线性模型系数不稳定，其影响不能很好地分解。
• 不同的线性模型对特征相关性的响应不同，各相关系数可能存在显著差异。
• 通过交叉验证循环对系数进行检测，给出了它们的稳定性概念。

脚本的总运行时间：(0分21.601秒)。

Download Python source code: plot_linear_model_coefficient_interpretation.py

Download Jupyter notebook: plot_linear_model_coefficient_interpretation.ipynb